题目内容
【题目】如图所示，“冰雪游乐场”滑道O点的左边为水平滑道，右边为高度h=3.2m的曲面滑道，左右两边的滑道在O点平滑连接．小孩乘坐冰车由静止开始从滑道顶端出发，经过O点后与处于静止状态的家长所坐的冰车发生碰撞，碰撞后小孩及其冰车恰好停止运动．已知小孩和冰车的总质量m=30kg，家长和冰车的总质量为M=60kg，人与冰车均可视为质点，不计一切摩擦阻力，取重力加速度g=10m/s2 ， 求：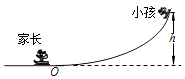
（1）小孩乘坐冰车经过O点时的速度大小；
（2）碰撞后家长和冰车共同运动的速度大小；
（3）碰撞过程中小孩和家长（包括各自冰车）组成的系统损失的机械能．
【答案】
（1）解：设小孩经过O点时的速度大小为v0，小孩乘坐冰车由曲面下滑的过程，由机械能守恒定律有
解得：v0= 
= 
=8m/s
答：小孩乘坐冰车经过O点时的速度大小是8m/s
（2）解：碰撞过程中小孩和家长（包括各自冰车）组成的系统动量守恒，设碰撞后家长的速度大小为v1，取向左为正方向，由动量守恒定律得
mv0=Mv1
解得 v1= 
v0= 
×8=4m/s
答：碰撞后家长和冰车共同运动的速度大小是4m/s
（3）解：设系统损失的机械能为△E，则 
= 
﹣ 
=480J
答：碰撞过程中小孩和家长（包括各自冰车）组成的系统损失的机械能是480J
【解析】（1）小孩乘坐冰车由曲面下滑的过程，只有重力做功，其机械能守恒，由机械能守恒定律求小孩乘坐冰车经过O点时的速度大小；（2）对于碰撞过程，小孩和家长（包括各自冰车）组成的系统动量守恒，由动量守恒定律求碰撞后家长和冰车共同运动的速度大小；（3）碰撞过程中小孩和家长（包括各自冰车）组成的系统损失的机械能等于碰撞前后机械能的差，由能量守恒定律求解．
练习册系列答案
相关题目
