��Ŀ����
����Ŀ����г�˶��������о�����һ�ֵ����˶���ʽ��
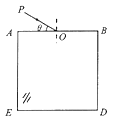
��1��һ���ʵ�����е��������Ļظ�����ƫ��ƽ��λ�õ�λ�ƴ�С�����ȣ����ҷ�����λ�Ʒ����෴�������ж����Ǽ�г�˶�����ͼ1��ʾ������������ϵ���ֱ�Ϊk1��k2�����ʵ������ڹ⻬��ˮƽ���ϣ����ɵ����˹̶����м��һ����Ϊm��С��ʱ�����ɾ�����ԭ�����ֽ�С���ظ�����һ�ξ�����ɿ���С����OΪƽ��λ�������˶�������ݴ�֤����С���������˶��Ǽ�г�˶���
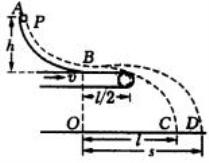
��2�������������Իظ�����ƫ��ƽ��λ�õ�λ�ƹ�ϵ���ж�һ���˶��Ƿ�Ϊ��г�˶�������ʵ��г�˶�Ҳ����һЩ�������������г�˶��ʵ���˶��ٶ�v����ƫ��ƽ��λ�õ�λ��x֮��Ĺ�ϵ�Ͷ����Ա�ʾΪv2=v02��ax2 �� ����v0Ϊ���ʵ�ͨ��ƽ��λ��ʱ��˲ʱ�ٶȣ�aΪ��ϵͳ�����ͳ�ʼ�����������IJ���ij���������֤����ͼ2��С����˶�Ҳ����������ϵ����˵�����ϵʽ�е�a����Щ�������йأ���֪���ɵĵ������ܿ��Ա���Ϊ ![]() ������k�ǵ��ɵľ���ϵ����x�ǵ��ɵ��α�����
������k�ǵ��ɵľ���ϵ����x�ǵ��ɵ��α�����
��3��һ�ʵ���˳ʱ�뷽�����ٶ�v0���뾶ΪR������Բ���˶�����ͼ��ʾ�����ϵڣ�2�����е���Ϣ��������֤С����x�����ϵķ��˶��Ƿ���ϼ�г�˶���һ������
���𰸡�
��1��֤������С������ƫ���λ��Ϊx��ѡȡ����Ϊ�������ɺ��˶��ɿɵã�С���ܵ��ĺ�������F��=����k1+k2��x
����k1��k2���dz���������С���ܵ��ĺ�������λ�Ƴ����ȣ�С������г��
��2��֤����С���˶��Ĺ����еĻ�е�ܰ���С��Ķ����뵯�ɵĵ������ܣ�С���˶��Ĺ�����ϵͳ�Ļ�е���غ㣬��С��ƫ��O������λ��ΪA����ͨ��ƽ��λ��ʱ��
![]()
��С������ƫ���λ��Ϊxʱ���ٶ�Ϊv����
![]()
���� ![]() =
= ![]()
��֪����a�����������ɵľ���ϵ���ĺͣ����ٶȵĴ�С�뿪ʼʱ������й�
��3��֤�������ʵ�ˮƽ�����λ��Ϊxʱ���ʵ��ٶ���x��֮��ļн���Ϊ�ȣ����ʵ���ٶ���x�᷽����y�᷽��ֽ���ͼ����
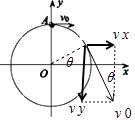
vy=v0cos��
���� ![]()
���ݺ��ٶ�����ٶȵĹ�ϵ��֪�� ![]()
�����ɵã� ![]() =
= ![]()
��֪С����x�����ϵķ��˶����ϼ�г�˶���һ������
֤��
����������1�����ݺ��˶��ɼ���д����С��ƫ��ƽ��λ�õ�λ�ƴ�СΪxʱ������F���ı���ʽ����2������С������г�˶�ʱ�Ļ�е���غ㼴��д������3�����ʵ���˶����������x������y����ֽ⣬����ٶȵķֽ��ϵ����֤����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�