题目内容
在与x轴平行的匀强电场中，一带电量为1.0×10-8库仑、质量为2.5×10-3千克的物体在光滑水平面上沿着x轴作直线运动，其位移与时间的关系是x=0.16t-0.02t2，式中x以米为单位，t以秒为单位．从开始运动到5秒末物体所经过的路程为________米，克服电场力所作的功为________焦耳．
0.34 30×10-5
分析：根据位移与时间的关系式可以得出物体的初速度和加速度，从而求出物体速度为0的时刻，也求出了物体减速的时间和路程，再根据反向做初速度为0的匀加速直线运动求出第5s末的速度和第5s内的位移，从而求出整个过程中物体通过的路程，再根据动能定理求出电场力对物体所做的功．而克服电场力所做的功等于电场力所做功的绝对值．
解答：根据x=0.16t-0.02t2=v0t+
at2可知，故有v0=0.16m/s，a=-0.02，a=-0.04m/s2，
故物体速度减小到0的时间为t=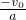
=
=4s
故物体在前4s的位移x1=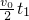
=0.08×4=0.32m，
第5s物体反向加速，其第5s内t通过的位移x2=
=0.02m，
故物体在前5s通过的路程x=x1+x2=0.34m．
物体从4s末开始做初速度为0的匀加速直线运动，加速度大小为0.04m/s2，故物体在第5s末的速度v=at=0.04×1=0.04m/s．
根据动能定理W=
-
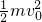=×2.5×10-3×0.042-×2.5×10-3×0.162=-30×10-5J
故克服电场力作的功为30×10-5J．
故答案为：0.34，30×10-5．
点评：物体做折线运动时一定要注意求解速度为0的时刻，这是我们求解位移，速度必须利用的条件．
分析：根据位移与时间的关系式可以得出物体的初速度和加速度，从而求出物体速度为0的时刻，也求出了物体减速的时间和路程，再根据反向做初速度为0的匀加速直线运动求出第5s末的速度和第5s内的位移，从而求出整个过程中物体通过的路程，再根据动能定理求出电场力对物体所做的功．而克服电场力所做的功等于电场力所做功的绝对值．
解答：根据x=0.16t-0.02t2=v0t+
at2可知，故有v0=0.16m/s，a=-0.02，a=-0.04m/s2，故物体速度减小到0的时间为t=
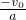==4s故物体在前4s的位移x1=
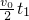=0.08×4=0.32m，第5s物体反向加速，其第5s内t通过的位移x2=
=0.02m，故物体在前5s通过的路程x=x1+x2=0.34m．
物体从4s末开始做初速度为0的匀加速直线运动，加速度大小为0.04m/s2，故物体在第5s末的速度v=at=0.04×1=0.04m/s．
根据动能定理W=
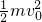-=×2.5×10-3×0.042-×2.5×10-3×0.162=-30×10-5J故克服电场力作的功为30×10-5J．
故答案为：0.34，30×10-5．
点评：物体做折线运动时一定要注意求解速度为0的时刻，这是我们求解位移，速度必须利用的条件．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
在与x轴平行的匀强电场中，一带电量为+2×10-6C、质量为4×10-2kg的带电物体在绝缘光滑水平面上沿着+x轴方向做直线运动，其位移随时间的变化规律是x=0.3t-0.05t2，式中x、t均用国际单位制的基本单位．求：