Question

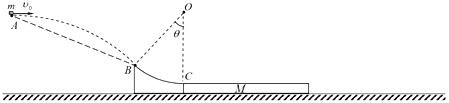
【题目】如图所示，一根光滑绝缘细杆与水平面成α＝30°角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中，场强E＝2×104 N/C.在细杆上套有一个带电荷量为q＝－×10-5 C、质量为m＝3×10-2 kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下，并从B点进入电场，小球在电场中滑至最远处的C点.已知AB间距离x1＝0.4 m，取g＝10 m/s2.求：

（1）小球在B点的速度vB的大小；

（2）小球进入电场后滑行的最大距离x2；

（3）试画出小球从A点运动到C点过程的v－t图像.

Answer 1

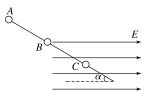
【答案】（1）2 m/s（2）0.4 m（3）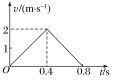

【解析】

（1）小球在AB段滑动过程中，由机械能守恒得：

mgx1sin α＝mvB2

可得

vB＝2 m/s.

（2）小球进入匀强电场后，在电场力和重力的作用下做匀减速运动，由牛顿第二定律得：

|q|Ecos α－mgsin α＝ma2

得

a2＝5 m/s2

小球进入电场后还能滑行到最远处C点，

vB2＝2a2x2

得：

x2＝0.4 m.

（3）小球从A到B和从B到C的两段位移的平均速度分别为

vAB＝

vBC＝，

x1＋x2＝t

可得

t＝0.8 s

v－t图像如图所示，