��Ŀ����
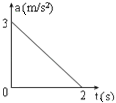
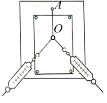
����Ŀ����ͼ��ʾ����A����v0=4m/s ��ˮƽ�ٶ��׳�һ����m=1kg��С��飨����Ϊ�ʵ㣩��������˶���B��ʱ��ǡ�������߷������̶��ڵ����ϵĹ⻬Բ�����BC�����й��C������ˮƽ��С���ͨ��Բ���������6m/s���ٶȻ�����C��ȸߡ���ֹ�ڴֲ�ˮƽ��ij�ľ��M�ϣ���֪��ľ�������M=2kg������볤ľ��֮��Ķ�Ħ��������1=0.5����ľ��������Ķ�Ħ��������2=0.1��OB����ֱ����OC��ļн���=37����ȡg=10m/s2��sin37��=0.6��cos37��=0.8����
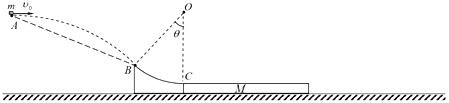
(1)��С����˶���B��ʱ���ٶȣ�
(2)��С���ǡ�ò�������ľ�壬����龰����С��黬�ϳ�ľ���𡢵��������ն�ͣ������ȫ�����У�����֮���Ħ���������Ĵ����ͣ�
���𰸡�(1) ![]() ��B��ʱ���ٶȷ�����ˮƽ�����37�� (2)
��B��ʱ���ٶȷ�����ˮƽ�����37�� (2) ![]()
��������
��1���ֽ�vB���ã�![]()
���εã�![]()
��B��ʱ���ٶȷ�����ˮƽ�����37��
��2����![]() ����ľ�彫�ڵ����ϻ��У���
����ľ�彫�ڵ����ϻ��У���
�������![]() ����
���� ![]()
�Գ�ľ���У�![]() ����
���� ![]()
�����Ǿ���ʱ��t������![]() �����У�
������
![]() ��
��
��ã�![]() ��
��![]()
���С�������Ի����У�![]() ��
��
��![]()
��Գ�ľ������Ի����У�![]() ��
��
��![]()
���ٺ�������һ������˶�����ϵͳ�У�![]() ��
��![]() �������Ǽ��Ħ����
�������Ǽ��Ħ����![]() �����Լ��������֮��������Ծ�ֹһ������ͣ�£��˹��������Ǽ�ľ�Ħ�����Զѷ�����һ����С��ȡ�һ��һ����������Ϊ��.
�����Լ��������֮��������Ծ�ֹһ������ͣ�£��˹��������Ǽ�ľ�Ħ�����Զѷ�����һ����С��ȡ�һ��һ����������Ϊ��.
������������С��黬�ϳ�ľ���𣬵���������ͣ������ȫ�����У�����֮���Ħ���������Ĵ�����![]()

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�