题目内容
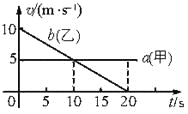
【题目】如图所示,长度l=18.75m的木板A置于倾角为θ=37°的足够长粗糙斜面上,木板与斜面间的动摩擦因数μ1=0.5木板A的上表面由粗糙面bc和光滑面cd两段组成,bc段的长度为4m;可视为质点的物块B放在木板最上端的b点,物块B与木板bc段的动摩擦因数μ2=![]() 现将A、B由静止开始释放,此时刻为计时起点。已知木板A和物块B的质量相同,设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2。
现将A、B由静止开始释放,此时刻为计时起点。已知木板A和物块B的质量相同,设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2。
求:(1)物块B滑到木板上c点所需要的时间t1;
(2)木板A速度减为零时,物块B的速度大小;
(3)物块B在木板A上运动的总时间t。

【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
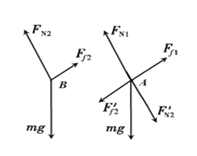
由滑动摩擦力公式和力的平衡条件得![]() ,
,![]() ,
,![]()
![]() ,规定沿斜面向下为正,设A和B的加速度分别为
,规定沿斜面向下为正,设A和B的加速度分别为![]() 和
和![]() ,由牛顿第二定律得:
,由牛顿第二定律得:![]() ,
,![]() ,解得:
,解得:![]()
由运动关系得:![]() ,解得:
,解得:![]()
(2)在![]() 时,设A和B的速度分别为
时,设A和B的速度分别为![]() 和
和![]() ,则
,则![]() ,
,![]() ,2s后,设A和B的加速度分别为
,2s后,设A和B的加速度分别为![]() 和
和![]() ,此时A与B之间摩擦力为0,同理可得
,此时A与B之间摩擦力为0,同理可得![]() ,
,![]() ,由于
,由于![]() ,可知A做减速运动,设经过时间
,可知A做减速运动,设经过时间![]() ,A的速度减为零,则有
,A的速度减为零,则有![]() ,此时B的速度
,此时B的速度![]() ,解得
,解得![]()
(3)在![]() 时间内,B相对A运动的距离为
时间内,B相对A运动的距离为
![]() =12m<27m,因此此后A静止不动,B继续在A上滑动,设再经过时间
=12m<27m,因此此后A静止不动,B继续在A上滑动,设再经过时间![]() 后B离开A,则有
后B离开A,则有![]() ,解得:
,解得:![]() ,则B在A上运动的总时间
,则B在A上运动的总时间![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目