题目内容
【题目】如图所示,区域Ⅰ内有电场强度为E=2![]() 104N/C、方向竖直向上的匀强电场;区域II中有一光滑绝缘圆弧轨道,轨道半径为R=2m,轨道在A点的切线与水平方向成60°角,在B点的切线与竖直线CD垂直;在区域Ⅲ有一宽为d=3m的有界匀强电场,电场强度大小未知,方向水平向右.一质量为m=0.4kg、带电荷量为q= -2
104N/C、方向竖直向上的匀强电场;区域II中有一光滑绝缘圆弧轨道,轨道半径为R=2m,轨道在A点的切线与水平方向成60°角,在B点的切线与竖直线CD垂直;在区域Ⅲ有一宽为d=3m的有界匀强电场,电场强度大小未知,方向水平向右.一质量为m=0.4kg、带电荷量为q= -2![]() 10-4C的小球(质点)从左边界O点正上方的M点以速度v0=2m/s水平射入区域I,恰好从A点沿圆弧轨道切线进入轨道且恰好不能从Ⅲ区域中电场的右边界穿出,(取g=10m/s2)求:
10-4C的小球(质点)从左边界O点正上方的M点以速度v0=2m/s水平射入区域I,恰好从A点沿圆弧轨道切线进入轨道且恰好不能从Ⅲ区域中电场的右边界穿出,(取g=10m/s2)求:
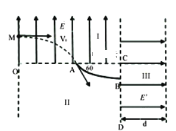
(1)OM的长L
(2)区域Ⅲ中电场的电场强度大小E′
【答案】(1)L=0.3m(2)E′=1.2![]() 104N/C
104N/C
【解析】
(1)小球在区域I中做类平抛运动,结合A点的速度方向和初速度求出竖直分速度,根据牛顿第二定律求出竖直方向上的加速度,结合速度位移公式求出L的长度;
(2)根据动能定理求出小球到达B点时的速度。小球在区域III中水平方向上做匀减速运动,结合牛顿第二定律和速度位移公式求出区域III的电场强度。
(1) 小球在区域 I中做类平抛运动,设小球在A点的速度为vA,竖直分速度为vy,则有:
![]()
vy=v0tan60°=![]()
由牛顿第二定律可得:a=![]()
由匀变速直线运动的速度位移公式得:vy2=2aL
解得:L=0.3m;
(2) 在区域 II中,由图可得,由A至B下降的高度为![]() ,则由A到B,根据动能定理得:
,则由A到B,根据动能定理得:
![]()
解得:vB=6m/s
在区域 III中,小球在水平方向做匀减速直线运动,到达右边界时水平速度刚好减为零
由匀变速直线运动的速度位移公式得:vB2=2![]()
解得:E′=1.2×104N/C。

【题目】竖直升降电梯经过启动、匀速运行和制动三个过程,从低楼层到达高楼层,启动和制动可看作是匀变速直线运动电梯竖直向上运动过程中速度的变化情况如表:
t/s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
v/(ms-1) | 0 | 2.0 | 4.0 | 5.0 | 5.0 | 5.0 | 5.0 | 5.0 | 4.0 | 3.0 | 2.0 | 1.0 | 0 |
下列说法企确的是( )
A. 前5秒电梯的位移为![]() B. 前5秒电梯的位移为
B. 前5秒电梯的位移为![]()
C. 电梯从第7秒开始减速D. 电梯减速的加速度大小为![]()