题目内容
17.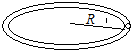 如图,水平放置的光滑固定圆形轨道半径为R,质量为m的小球由静止起从轨道最右端附近处处释放,在一个大小始终为$\frac{mg}{5}$、水平向左的恒力F作用下沿轨道运动,求小球运动到轨道最左端时对轨道的作用力.
如图,水平放置的光滑固定圆形轨道半径为R,质量为m的小球由静止起从轨道最右端附近处处释放,在一个大小始终为$\frac{mg}{5}$、水平向左的恒力F作用下沿轨道运动,求小球运动到轨道最左端时对轨道的作用力.
分析 研究小球从最右端到最左端的过程,运用动能定理求解小球到最左端的速度,
根据牛顿第二定律研究小球运动到轨道最左端,得出小球对轨道的作用力.
解答 解:研究小球从最右端到最左端的过程,运用动能定理得
F×2R=$\frac{1}{2}$mV2,
所以V=$\sqrt{\frac{4FR}{m}}$=$\sqrt{0.8Rg}$
根据牛顿第二定律研究小球运动到轨道最左端,
水平方向:N1-F=m$\frac{{v}^{2}}{R}$,
N1=F+m$\frac{{v}^{2}}{R}$=mg.
竖直方向:N2=mg,
所以轨道对小球作用力大小N=$\sqrt{{{N}_{2}^{2}+N}_{1}^{2}}$=$\sqrt{2}$mg,
根据牛顿第三定律得小球运动到轨道最左端时对轨道的作用力大小是$\sqrt{2}$mg,方向斜向左下方与水平成45°角.
答:小球运动到轨道最左端时对轨道的作用力大小是$\sqrt{2}$mg,方向斜向左下方与水平成45°角.
点评 本题考查了牛顿第二定律和动能定理的综合运用,知道最左端向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
5. 如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
 如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )
如图,A、B两物体用一根跨过定滑轮的细系住,置于固定地面上的直角斜面体两边相同高度上,处于静止状态,若不计摩擦,剪断细绳后下面说法正确的有( )| A. | 着地时两物体速度相同 | B. | 着地时两物体机械能相同 | ||
| C. | 着地时两物体所受重力的功率相同 | D. | 两物体沿斜面滑行的时间相同 |
2.关于电动势,下列说法错误的是( )
| A. | 电源电动势等于电源两极间的电压 | |
| B. | 电源电动势与外电路的组成无关,只与电源本身有关 | |
| C. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| D. | 电动势在数值上等于非静电力把1C的正电荷在电源内从负极已送到正极所做的功 |
 两平行板间有水平匀强电场,一根长为L,不可伸长的不导电细绳的一端连着一个质量为 m、带电量为q的小球,另一端固定于O点.把小球拉起直至细线与电场线平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ,求:(θ=37°且sin37°=$\frac{3}{5}$ cos37°=$\frac{4}{5}$)
两平行板间有水平匀强电场,一根长为L,不可伸长的不导电细绳的一端连着一个质量为 m、带电量为q的小球,另一端固定于O点.把小球拉起直至细线与电场线平行,然后无初速度释放.已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ,求:(θ=37°且sin37°=$\frac{3}{5}$ cos37°=$\frac{4}{5}$)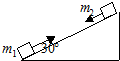 如图表光滑斜面长为2m,倾角为30°,质量为0.3Kg的物体m2从斜面顶部由静止下滑,质量为0.2Kg的另一物体m1同时从斜面底端以5m/s的初速向上运动,两物体相碰后即粘在一起,则碰撞后经过0.8s两物体到达斜面底端.
如图表光滑斜面长为2m,倾角为30°,质量为0.3Kg的物体m2从斜面顶部由静止下滑,质量为0.2Kg的另一物体m1同时从斜面底端以5m/s的初速向上运动,两物体相碰后即粘在一起,则碰撞后经过0.8s两物体到达斜面底端. 如图是一匀强电场,在电场中有M、N、P三点,M、N的连线与电场线方向平行,P、N的连线与电场线方向垂直,P、M的连线与M、N的连线的夹角θ=37°.已知MP间的距离s=30cm.现将一个电荷量为q=-4×10-8C的点电荷从M点沿MP连线移到P点,需克服电场力做功2.4×10-6J.(sin37°=0.6,cos37°=0.8)试求:
如图是一匀强电场,在电场中有M、N、P三点,M、N的连线与电场线方向平行,P、N的连线与电场线方向垂直,P、M的连线与M、N的连线的夹角θ=37°.已知MP间的距离s=30cm.现将一个电荷量为q=-4×10-8C的点电荷从M点沿MP连线移到P点,需克服电场力做功2.4×10-6J.(sin37°=0.6,cos37°=0.8)试求: