题目内容
9. 如图所示,传送带与地面间的倾角为θ=37°,A,B之间的长度为L=16m,传送带以速率v=10m/s逆时针运动,在传送带A端无初速度放一个质量为m=0.5kg的物体(可视为质点),它与传送带之间的动摩擦因数μ=0.5.
如图所示,传送带与地面间的倾角为θ=37°,A,B之间的长度为L=16m,传送带以速率v=10m/s逆时针运动,在传送带A端无初速度放一个质量为m=0.5kg的物体(可视为质点),它与传送带之间的动摩擦因数μ=0.5.求:(1)物体刚放到传送带上摩擦力的大小及方向;
(2)物体从A端运动到B端需要的时间.
(g取10m/s2,sin37°≈0.6,cos37°≈0.8)
分析 (1)物体刚放上传送带,摩擦力的方向沿传送带向下,由滑动摩擦力的公式即可求出摩擦力的大小;
(2)根据牛顿第二定律求出物体的加速度,结合运动学公式求出速度达到传送带速度时的时间和位移,由于重力沿斜面方向的分力大于滑动摩擦力,速度相等后,滑动摩擦力沿斜面向上,根据牛顿第二定律求出物体的加速度,结合位移时间公式求出剩余段匀加速运动的时间,从而得出物体从A运动到B的时间.
解答 解:(1)开始时,物体相对传送带沿斜面向上滑,所以摩擦力的方向向下;由公式得:
f=μmgcosθ=0.5×0.5×10×0.8=2N
(2)由牛顿第二定律,开始时:${a}_{1}=\frac{mgsinθ+μmgcosθ}{m}$=gsinθ+μgcosθ=10×0.6+0.5×10×0.8=10m/s2,
当物体与传送带相对静止时,物体的位移:${x}_{1}=\frac{{v}^{2}}{2{a}_{1}}=\frac{100}{2×10}m=5m$;t1=$\frac{v}{{a}_{1}}=\frac{10}{10}s$=1s
则:x2=16-5=11m
因为mgsinθ>μmgcosθ,物体与传送带不能保持相对静止,
此时,物体的加速度 ${a}_{2}=\frac{mgsinθ-μmgcosθ}{m}$=gsinθ-μgcosθ=10×0.6-0.5×10×0.8=2m/s2.
则:${x_2}=vt+\frac{1}{2}{a_2}{t^2}$;
代入数据解得:t2=1s;
故共耗时t=t1+t2=2s.
答::(1)物体刚放到传送带上摩擦力的大小是2N,方向沿斜面向下;
(2)物体从A运动到B需时间为2s.
点评 解决本题的关键知道物体在传送带上的运动规律,结合运动学公式和牛顿第二定律综合求解,难度中等.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案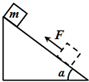 如图所示,质量为m物体从倾角α=30°光滑斜面的顶端由静止下滑,经时间t速率为v1,此时施加平行于斜面向上的恒力F,又经时间t物体回到出发点,速率为v2,已知下滑过程中物体始终未脱离斜面,则下列说法正确的是( )
如图所示,质量为m物体从倾角α=30°光滑斜面的顶端由静止下滑,经时间t速率为v1,此时施加平行于斜面向上的恒力F,又经时间t物体回到出发点,速率为v2,已知下滑过程中物体始终未脱离斜面,则下列说法正确的是( )| A. | v2:v1=1:1 | B. | v2:v1=2:1 | C. | $\frac{F}{mg}$=2:1 | D. | $\frac{F}{mg}$=3:1 |
| A. | 1×10-2N | B. | 1×10-3N | C. | 1×10-4N | D. | 1×10-5N |
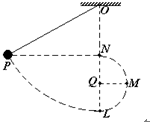 如图,一细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球.L点是小球下垂时的平衡位置,Q点代表一固定在墙上的细长钉子,位于OL直线上.N点在Q点正上方,且QN=QL,M点与Q点等高,现将小球从竖直位置(保持绳绷直)拉开到与N等高的P点,释放后任其向L摆动.运动过程中空气阻力可忽略不计.小球到达L后,因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动.在这以后( )
如图,一细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球.L点是小球下垂时的平衡位置,Q点代表一固定在墙上的细长钉子,位于OL直线上.N点在Q点正上方,且QN=QL,M点与Q点等高,现将小球从竖直位置(保持绳绷直)拉开到与N等高的P点,释放后任其向L摆动.运动过程中空气阻力可忽略不计.小球到达L后,因细绳被长钉挡住,将开始沿以Q为中心的圆弧继续运动.在这以后( )| A. | 小球向右摆到M点,然后就摆回来 | |
| B. | 小球向右摆到M和N之间圆弧上某点处,然后斜抛运动 | |
| C. | 小球沿圆弧摆到N点,然后竖直下落 | |
| D. | 小球将绕Q点旋转,直到细绳完全缠绕在钉上为止 |
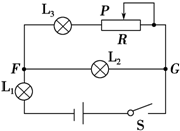 如图所示的电路,L1、L2、L3是3只小电灯,R是滑动变阻器,开始时,它的滑片P位于中点位置.当S闭合时,3只小电灯都发光.现使滑动变阻器的滑片P向右移动时,则小电灯L1、L2、L3的变化情况( )
如图所示的电路,L1、L2、L3是3只小电灯,R是滑动变阻器,开始时,它的滑片P位于中点位置.当S闭合时,3只小电灯都发光.现使滑动变阻器的滑片P向右移动时,则小电灯L1、L2、L3的变化情况( )| A. | L1变亮 | B. | L2变亮 | C. | L3变亮 | D. | L1、L2、L3均变亮 |
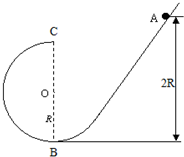 如图所示,倾斜轨道的下端与半径为R的圆轨道平滑连接,现在使小球从弧形轨道上端距地面2R的A点由静止滑下,进入圆轨道后沿圆轨道运动,轨道摩擦不计.试求:
如图所示,倾斜轨道的下端与半径为R的圆轨道平滑连接,现在使小球从弧形轨道上端距地面2R的A点由静止滑下,进入圆轨道后沿圆轨道运动,轨道摩擦不计.试求: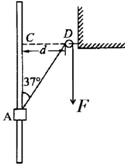 如图所示,光滑固定的竖直杆上套有一个质量为m的小物块A,不可伸长的轻质细绳左端与物块A 相连,绕过固定在墙壁上、大小可忽略的定滑轮D后,右端作用恒定拉力F,虚线CD水平,间距为d,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.现瞬间调整绳右端的拉力为 F1=4F,使得物块从图示位置开始向上运动并通过C点,不计摩擦和空气阻力,重力加速度为g,cos37°=0.8,sin37°=0.6.求:
如图所示,光滑固定的竖直杆上套有一个质量为m的小物块A,不可伸长的轻质细绳左端与物块A 相连,绕过固定在墙壁上、大小可忽略的定滑轮D后,右端作用恒定拉力F,虚线CD水平,间距为d,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.现瞬间调整绳右端的拉力为 F1=4F,使得物块从图示位置开始向上运动并通过C点,不计摩擦和空气阻力,重力加速度为g,cos37°=0.8,sin37°=0.6.求: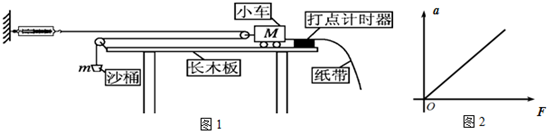
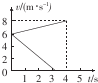 两个完全相同的物块A、B,质量均为m=1kg,沿同一粗糙水平面以相同的初速度从同一位置开始运动.它们速度随时间的变化关系如图所示,图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象.求:
两个完全相同的物块A、B,质量均为m=1kg,沿同一粗糙水平面以相同的初速度从同一位置开始运动.它们速度随时间的变化关系如图所示,图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象.求: