题目内容
4. 如图所示,光滑固定的竖直杆上套有一个质量为m的小物块A,不可伸长的轻质细绳左端与物块A 相连,绕过固定在墙壁上、大小可忽略的定滑轮D后,右端作用恒定拉力F,虚线CD水平,间距为d,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.现瞬间调整绳右端的拉力为 F1=4F,使得物块从图示位置开始向上运动并通过C点,不计摩擦和空气阻力,重力加速度为g,cos37°=0.8,sin37°=0.6.求:
如图所示,光滑固定的竖直杆上套有一个质量为m的小物块A,不可伸长的轻质细绳左端与物块A 相连,绕过固定在墙壁上、大小可忽略的定滑轮D后,右端作用恒定拉力F,虚线CD水平,间距为d,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止.现瞬间调整绳右端的拉力为 F1=4F,使得物块从图示位置开始向上运动并通过C点,不计摩擦和空气阻力,重力加速度为g,cos37°=0.8,sin37°=0.6.求:(1)恒力F的大小;
(2)物块A通过C处时的速度大小.
分析 (1)根据共点力平衡求的拉力
(2)从A到C的过程中根据动能定理求的物体达到C点的速度
解答 解:(1)对物体A受力分析,根据共点力平衡可得
Fcos37°-mg=0
解得 F=1.25mg
(2)动A到C由动能定理可得
${F_1}(\frac{d}{{sin{{37}^o}}}-d)-mgdcot{37^o}=\frac{1}{2}m{v^2}$
解得$v=2\sqrt{gd}$
答:(1)恒力F的大小为1.25mg;
(2)物块A通过C处时的速度大小为$2\sqrt{gd}$
点评 本题第一问问直接根据平衡条件列式求解;第二问运用动能定理列式求解,较难

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
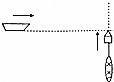
15.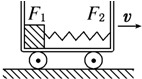 如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )
如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )
 如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )
如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )| A. | 车向右匀加速直线运动,F2变大 | B. | 车向右匀加速直线运动,F2不变 | ||
| C. | 车向右匀减速直线运动,F2变小 | D. | 车向右匀减速直线运动,F2不变 |
12.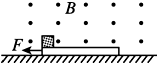 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块开始做加速度减小的变加速运动,最后做速度为10 m/s的匀速运动 | |
| C. | 木板先做加速度为2m/s2的匀加速运动,再做加速度增大的运动,最后做加速度为3 m/s2的匀加速运动 | |
| D. | t=3s后滑块和木板有相对运动 |
19.试根据表中数据,归纳出球形物体所受的空气阻力f与球的速度v及球的半径r的关系式为( )
| A. | f=10vr(N) | B. | f=10vr2(N) | C. | f=5vr(N) | D. | f=5vr2(N) |
13.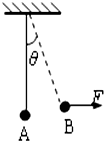 如图所示,细线挂着质量为m的小球静止在位置A,现用水平恒力F将其从位置A向右拉到位置B点,此时线与竖直方向夹角为θ,且tanθ=$\frac{F}{mg}$.则小球在从A到B的过程中( )
如图所示,细线挂着质量为m的小球静止在位置A,现用水平恒力F将其从位置A向右拉到位置B点,此时线与竖直方向夹角为θ,且tanθ=$\frac{F}{mg}$.则小球在从A到B的过程中( )
 如图所示,细线挂着质量为m的小球静止在位置A,现用水平恒力F将其从位置A向右拉到位置B点,此时线与竖直方向夹角为θ,且tanθ=$\frac{F}{mg}$.则小球在从A到B的过程中( )
如图所示,细线挂着质量为m的小球静止在位置A,现用水平恒力F将其从位置A向右拉到位置B点,此时线与竖直方向夹角为θ,且tanθ=$\frac{F}{mg}$.则小球在从A到B的过程中( )| A. | 恒力F做的功大于小球重力势能的增量 | |
| B. | 小球在B点时的加速度、速度均为零 | |
| C. | 若继续保持恒力F的作用,线与竖直方向的夹角最大可为2θ | |
| D. | 若小球在B时将力F撤去,小球来回摆动的摆角将大于θ |
14.如图是某交流电的电压i随时间t按正弦规律变化的图象.由图可知,该交变电流( 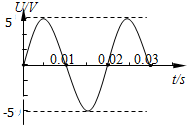

| A. | 频率为50Hz | B. | 周期为0.01s | C. | 交流最大值为$5\sqrt{2}$A | D. | 电流有效值为5A |
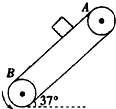 如图所示,传送带与地面间的倾角为θ=37°,A,B之间的长度为L=16m,传送带以速率v=10m/s逆时针运动,在传送带A端无初速度放一个质量为m=0.5kg的物体(可视为质点),它与传送带之间的动摩擦因数μ=0.5.
如图所示,传送带与地面间的倾角为θ=37°,A,B之间的长度为L=16m,传送带以速率v=10m/s逆时针运动,在传送带A端无初速度放一个质量为m=0.5kg的物体(可视为质点),它与传送带之间的动摩擦因数μ=0.5.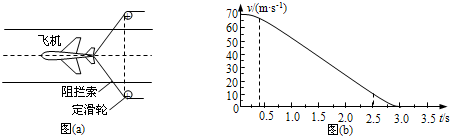 “歼-15”是我国研制的第三代战斗机,2012年11月24日,“歼-15”舰载机在“辽宁号”航空母舰上成功着舰.图a为利用阻拦系统让舰载机在飞行甲板上快速停止的原理示意图.舰载机着舰并成功钩住阻拦索后,飞机的动力系统立即关闭,阻拦系统通过阻拦索对飞机施加一作用力,使舰载机在甲板上短距离滑行后停止,某次降落,以舰载机着舰为计时零点,舰载机在t=0.4s时恰好钩住阻拦索中间位置,其着舰到停止的速度-时间图线如图(b)所示.如果无阻拦索,舰载机从着舰到停止需要的滑行距离约为1000m.已知航母始终静止,“歼-15”舰载机的质量为2.0×104kg,重力加速度的大小为g=10m/s2.求:
“歼-15”是我国研制的第三代战斗机,2012年11月24日,“歼-15”舰载机在“辽宁号”航空母舰上成功着舰.图a为利用阻拦系统让舰载机在飞行甲板上快速停止的原理示意图.舰载机着舰并成功钩住阻拦索后,飞机的动力系统立即关闭,阻拦系统通过阻拦索对飞机施加一作用力,使舰载机在甲板上短距离滑行后停止,某次降落,以舰载机着舰为计时零点,舰载机在t=0.4s时恰好钩住阻拦索中间位置,其着舰到停止的速度-时间图线如图(b)所示.如果无阻拦索,舰载机从着舰到停止需要的滑行距离约为1000m.已知航母始终静止,“歼-15”舰载机的质量为2.0×104kg,重力加速度的大小为g=10m/s2.求: