题目内容
20. 如图所示,倾斜轨道的下端与半径为R的圆轨道平滑连接,现在使小球从弧形轨道上端距地面2R的A点由静止滑下,进入圆轨道后沿圆轨道运动,轨道摩擦不计.试求:
如图所示,倾斜轨道的下端与半径为R的圆轨道平滑连接,现在使小球从弧形轨道上端距地面2R的A点由静止滑下,进入圆轨道后沿圆轨道运动,轨道摩擦不计.试求:(1)小球在最低点B时对轨道的压力大小;
(2)若使小球能过圆轨道最高点C,则释放小球时,A′点距离地面的高度至少是多少?
分析 (1)对小球从A到B过程运用动能定理列式求解末速度;在B点,重力和支持力的合力提供向心力,根据牛顿第二定律列式求解支持力,再根据牛顿第三定律得到压力;
(2)考虑临界情况,在C点,重力提供向心力,得到C点的速度;对从A′点到C过程,根据动能定理列式;最后联立求解即可.
解答 解:(1)小球从A到B的过程中,由动能定理得:
$mg•2R=\frac{1}{2}m{v^2}$
得:v=2$\sqrt{gR}$
在最低点,根据牛顿第二定律,有:
${N_B}-mg=m\frac{v^2}{R}$
得:NB=5mg
根据牛顿第三定律:小球在最低点B时,对轨道的压力大小为5mg.
(2)设小球恰好能过C点,则在C点有:$mg=m\frac{{v}_{C}^{2}}{R}$.
设此时A′点距地面高度为h,则小球从A′到C的过程中,由机械能守恒定律得:
mgh=mg•2R+$\frac{1}{2}m{v}_{C}^{2}$
联立解得:
h=2.5R
答:(1)小球在最低点B时对轨道的压力大小为5mg;
(2)若使小球能过圆轨道最高点C,则释放小球时,A′点距离地面的高度至少是2.5R.
点评 本题关键是明确小球的受力情况和运动情况,结合动能定理、牛顿第二定律列式分析,基础题目.

练习册系列答案
相关题目
15.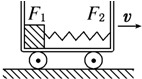 如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )
如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )
 如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )
如图所示,小车沿水平面做匀速直线运动,小车内光滑底面上有一物块被压缩的弹簧压向左壁.若车左壁受物块的压力F1变为0,则车的运动情况和车右壁受弹簧的压力F2的大小变化是( )| A. | 车向右匀加速直线运动,F2变大 | B. | 车向右匀加速直线运动,F2不变 | ||
| C. | 车向右匀减速直线运动,F2变小 | D. | 车向右匀减速直线运动,F2不变 |
12.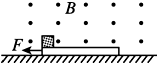 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
 如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )
如图所示,空间有一垂直于纸面的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速度放置一质量为0.1kg、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.t=0时对木板施加方向水平向左,大小为0.6N的恒力F,g取10m/s2,则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块开始做加速度减小的变加速运动,最后做速度为10 m/s的匀速运动 | |
| C. | 木板先做加速度为2m/s2的匀加速运动,再做加速度增大的运动,最后做加速度为3 m/s2的匀加速运动 | |
| D. | t=3s后滑块和木板有相对运动 |
 第22届冬季奥林匹克运动会于2014年02月07日~02月23日在俄罗斯联邦索契市举行,中国选手徐梦桃获得自由式滑雪女子空中技巧银牌.假设滑雪者的速度超过4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125.一滑雪者从倾角为θ=37°的坡顶A由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平雪地,最后停在C处,如图所示.不计空气阻力,坡长为L=26m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
第22届冬季奥林匹克运动会于2014年02月07日~02月23日在俄罗斯联邦索契市举行,中国选手徐梦桃获得自由式滑雪女子空中技巧银牌.假设滑雪者的速度超过4m/s时,滑雪板与雪地间的动摩擦因数就会由μ1=0.25变为μ2=0.125.一滑雪者从倾角为θ=37°的坡顶A由静止开始自由下滑,滑至坡底B(B处为一光滑小圆弧)后又滑上一段水平雪地,最后停在C处,如图所示.不计空气阻力,坡长为L=26m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求: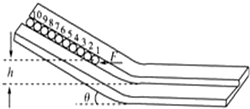 如图所示的木板由倾斜部分和水平部分组成,两部分之间由一段圆弧面相连接.在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在施加于1号球的水平外力F的作用下均静止,力F与圆槽在同一竖直面内,此时1号球球心距它在水平槽运动时的球心高度差为h.现撤去力F使小球开始运动,直到所有小球均运动到水平槽内.重力加速度为g.求:
如图所示的木板由倾斜部分和水平部分组成,两部分之间由一段圆弧面相连接.在木板的中间有位于竖直面内的光滑圆槽轨道,斜面的倾角为θ.现有10个质量均为m、半径均为r的均匀刚性球,在施加于1号球的水平外力F的作用下均静止,力F与圆槽在同一竖直面内,此时1号球球心距它在水平槽运动时的球心高度差为h.现撤去力F使小球开始运动,直到所有小球均运动到水平槽内.重力加速度为g.求: 如图所示,有一倾角为37°的固定斜面,斜面上有一质量为5kg的物体,该物体在拉力F 的作用下沿斜面向上做匀速直线运动.已知F=40N,方向与斜面的夹角也为37°(g 取10N/kg,sin37°=0.6,cos37°=0.8).求:
如图所示,有一倾角为37°的固定斜面,斜面上有一质量为5kg的物体,该物体在拉力F 的作用下沿斜面向上做匀速直线运动.已知F=40N,方向与斜面的夹角也为37°(g 取10N/kg,sin37°=0.6,cos37°=0.8).求: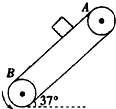 如图所示,传送带与地面间的倾角为θ=37°,A,B之间的长度为L=16m,传送带以速率v=10m/s逆时针运动,在传送带A端无初速度放一个质量为m=0.5kg的物体(可视为质点),它与传送带之间的动摩擦因数μ=0.5.
如图所示,传送带与地面间的倾角为θ=37°,A,B之间的长度为L=16m,传送带以速率v=10m/s逆时针运动,在传送带A端无初速度放一个质量为m=0.5kg的物体(可视为质点),它与传送带之间的动摩擦因数μ=0.5.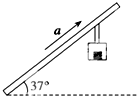 如图为用索道运输货物的情景,已知倾斜的索道与水平方向的夹角为37°,重物与车厢地板之间的动摩擦因数为0.30.当载重车厢沿索道向上加速运动时,重物与车厢仍然保持相对静止状态,重物对车厢内水平地板的正压力为其重力的1.15倍,sin 37°=0.6,cos 37°=0.8,那么这时重物对车厢地板的摩擦力大小为( )
如图为用索道运输货物的情景,已知倾斜的索道与水平方向的夹角为37°,重物与车厢地板之间的动摩擦因数为0.30.当载重车厢沿索道向上加速运动时,重物与车厢仍然保持相对静止状态,重物对车厢内水平地板的正压力为其重力的1.15倍,sin 37°=0.6,cos 37°=0.8,那么这时重物对车厢地板的摩擦力大小为( )