题目内容
如图8-3-5所示，粗细均匀的U形玻璃管如图放置，管的竖直部分长为20 cm，一端封闭，水平部分长40 cm，水平段管内长为20 cm的水银柱封住长35 cm的气柱.已知所封闭的气体温度为7 ℃，大气压强为75 cmHg，当管内温度升到351 ℃时管内空气柱的总长度是多少？（弯管部分体积忽略不计）
图8-3-5
图8-3-5
65cm.
温度升高时，气体体积增加，水银柱可能进入直管也可能溢出，所以要首先分析各临界状态的条件，然后针对具体情况计算.
设水银柱刚好与竖直管口平齐而正好不溢出，此时气柱高度为60 cm，设温度为T2.
以封闭气体为研究对象：
初状态：p1=p0="75" cmHg,l1="35" cm,T1="280" K
末状态：p2′="95" cmHg,l2="60" cm,T2=?
根据理想气体状态方程：
=
所以T2=
T1=
×280 K="608" K
即t2="(608-273)" ℃="335" ℃<351 ℃，所以水银柱会溢出.
设溢出后，竖直管内仍剩余水银柱长为h cm，则
初状态：p1="75" cmHg,l1="35" cm,T1="280" K
末状态：p′2="(75+h)" cmHg,l′2="(80-h)" cm,T′2="(351+273)" K="624" K
根据理想气体状态方程得：
=
即
=
h="15" cm
故管内空气柱的长度为l2′="(80-15)" cm=65cm.
设水银柱刚好与竖直管口平齐而正好不溢出，此时气柱高度为60 cm，设温度为T2.
以封闭气体为研究对象：
初状态：p1=p0="75" cmHg,l1="35" cm,T1="280" K
末状态：p2′="95" cmHg,l2="60" cm,T2=?
根据理想气体状态方程：
=所以T2=
T1=×280 K="608" K即t2="(608-273)" ℃="335" ℃<351 ℃，所以水银柱会溢出.
设溢出后，竖直管内仍剩余水银柱长为h cm，则
初状态：p1="75" cmHg,l1="35" cm,T1="280" K
末状态：p′2="(75+h)" cmHg,l′2="(80-h)" cm,T′2="(351+273)" K="624" K
根据理想气体状态方程得：
=即
=h="15" cm
故管内空气柱的长度为l2′="(80-15)" cm=65cm.
练习册系列答案
相关题目
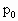＝76cmHg不变，管内有30cm长的水银柱将一部分空气封闭于封闭端，当管内空气为－17℃时，空气柱长40cm．
