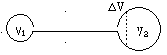题目内容
如图所示,粗细均匀一端封闭、一端开口的细玻璃管总长为100cm,中央折成直角,使它一半水平,一半竖直,外界大气压为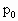 =76cmHg不变,管内有30cm长的水银柱将一部分空气封闭于封闭端,当管内空气为-17℃时,空气柱长40cm.
=76cmHg不变,管内有30cm长的水银柱将一部分空气封闭于封闭端,当管内空气为-17℃时,空气柱长40cm.

(1)当管内气体温度上升到30℃时,管内空气柱有多长?
(2)要将管内水银全部排空,管内气温至少应大于多少摄氏度?(假设温度上升是缓慢的)
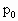 =76cmHg不变,管内有30cm长的水银柱将一部分空气封闭于封闭端,当管内空气为-17℃时,空气柱长40cm.
=76cmHg不变,管内有30cm长的水银柱将一部分空气封闭于封闭端,当管内空气为-17℃时,空气柱长40cm.
(1)当管内气体温度上升到30℃时,管内空气柱有多长?
(2)要将管内水银全部排空,管内气温至少应大于多少摄氏度?(假设温度上升是缓慢的)
(1) 45cm (2)T≥516.4L可全部排空水银.
本题的最高温度是否恰好在水银全部排空的时刻,极有可能成为意外的盲点,因为在排空水银的过程中压强在减小,排空的速度在加快,气体对外做功的速度也在加快,当然会引起内能减少的加快,如果做功的速度大于吸热的速度,温度就会降低,也就是说,温度的最高点应出现在做功的速度等于吸热的速度的那一刻.
(1)设水银恰好全部进入竖直管内,有:
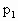 =(76+20)cmHg=96cmHg
=(76+20)cmHg=96cmHg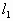 =40cm
=40cm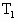 =(273-17)K=256K
=(273-17)K=256K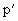 =(76+30)cmHg=106cmHg
=(76+30)cmHg=106cmHg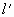 =50cm
=50cm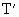 =?
=?据
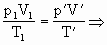
有
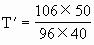 ×256K=353.4L
×256K=353.4L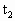 =80.3℃>30℃,故30℃时有水银在水平管内,设水银留有x长,有此时压强:
=80.3℃>30℃,故30℃时有水银在水平管内,设水银留有x长,有此时压强: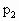 =(106-x)cmHg
=(106-x)cmHg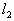 =(50-x)cm
=(50-x)cm据
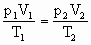
有
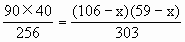
解得:x=5cm
所以:
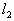 =(50-5)cm=45cm
=(50-5)cm=45cm(2)设管口还留有水银柱h cm时,温度为
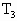 是排空过程中温度的极大值有:
是排空过程中温度的极大值有: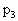 =(76-h)cmHg
=(76-h)cmHg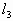 =(100-h)cm
=(100-h)cm据
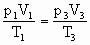
有
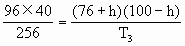
整理:
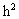 -24h+15
-24h+15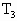 -7600=0
-7600=0方程有解有其判别式:Δ=242-4(15
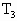 -7600)
-7600)解得:
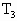 ≤516.4L
≤516.4L即当 T≥516.4L可全部排空水银.
温度上升时气体体积膨胀,水平管内的水银逐渐减少,竖直管内的水银逐渐增加,对30℃时水平管内有无水银需做出判断;要将管内水银全部排空,应计算管内温度的极大值,而这一极大值不一定是出现在气体恰好全部排空的时刻.
[思路一]设水银恰好全部进入竖直管内时,求此时的温度并与30℃时的温度相比,看水平管内此时是否留有水银,进一步求解管内气体温度上升到30℃时,管内空气柱有多长;排空水银的过程中,设温度的极大值出现在排空过程中的某一点,列方程即可分析求解温度的极大值.
[思路二]设当管内气体温度上升到30℃时,水平管内留有长x的水银柱,求出结果看是否合理,进而确定当管内气体温度上升到30℃时,管内空气柱有多长;排空水银的过程中,设温度的极大值出现在排空过程中的某一点,列方程即可分析求解温度的极大值.
[思路三]设被封气体体积保持不变,用p/T=Δp/ΔT可以计算出压强的增量值,也可确定当管内气体温度上升到30℃时,水平管内有无水银;排空水银的过程中,设温度的极大值出现在排空过程中的某一点,列方程即可分析求解温度的极大值.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目


 光滑斜面上,气缸A倒扣在水平地面上,气缸A和B内装有相同质量的同种气体,体积都为
光滑斜面上,气缸A倒扣在水平地面上,气缸A和B内装有相同质量的同种气体,体积都为 ,温度都为
,温度都为 ,如图所示,此时气缸A的气缸筒恰好对地面没有压力.设气缸内气体的质量远小于活塞的质量,大气对活塞的压力等于活塞重的1.5倍.
,如图所示,此时气缸A的气缸筒恰好对地面没有压力.设气缸内气体的质量远小于活塞的质量,大气对活塞的压力等于活塞重的1.5倍.
 ,气缸B内的气体的温度是多少?
,气缸B内的气体的温度是多少?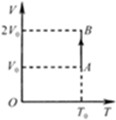
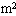 的气缸内,被质量可忽略不计的轻活塞封闭着一定质量的气体.气缸内有一质量为0.1kg的空心球.当活塞上面放2000N的重物时,空心球刚好对气缸底无压力,此时气缸内的温度为27℃;活塞上面所放重物减少1000N后,气缸内温度则下降为17℃.求此时空心球对气缸底的压力是多少.(设当时大气压强
的气缸内,被质量可忽略不计的轻活塞封闭着一定质量的气体.气缸内有一质量为0.1kg的空心球.当活塞上面放2000N的重物时,空心球刚好对气缸底无压力,此时气缸内的温度为27℃;活塞上面所放重物减少1000N后,气缸内温度则下降为17℃.求此时空心球对气缸底的压力是多少.(设当时大气压强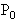 =1.0×
=1.0×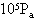 、取g=10m/
、取g=10m/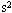 )
)
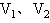 的两容器,用一根不导热的细管(体积可忽略不计)连通,如图所示.容器内充满空气,最初两容器都浸在温度为
的两容器,用一根不导热的细管(体积可忽略不计)连通,如图所示.容器内充满空气,最初两容器都浸在温度为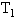 的水中,然后把容积为
的水中,然后把容积为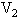 的容器用温度为
的容器用温度为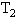 的水蒸汽包围,但容积为
的水蒸汽包围,但容积为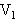 的容器仍保持原来温度.如果两个容器内空气的最初压强都为
的容器仍保持原来温度.如果两个容器内空气的最初压强都为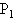 ,求最后两容器内空气的压强
,求最后两容器内空气的压强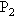 .(设容器的膨胀忽略不计)
.(设容器的膨胀忽略不计)