题目内容
12.如图1所示为“探究加速度与力、质量的关系”的实验装置示意图.砂和砂桶的质量为m,小车和砝码的总质量为M.实验中用砂和砂桶总重力的大小作为细线对小车拉力的大小.
(1)实验开始时需平衡摩擦,某同学的操作如下:将长木板的一端垫起适当的高度,小车后端连着已经穿过打点计时器的纸带,前端连着挂有砂和砂桶并跨过滑轮的细线,轻推小车,观察小车是否做匀速直线运动.此平衡摩擦的方法错(填“对”或“错”).
(2)实验中还需满足m远小于 M(填“远小于”或“远大于”).
(3)如图2所示,某同学在做实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.1s,其中S1=7.05cm,S2=7.68cm,S3=8.33cm,S4=8.95cm,S5=9.61cm,S6=10.26cm,则A点处的瞬时速度大小是0.86m/s,加速度的大小是0.64m/s2.(保留两位有效数字)
分析 (1、2)小车在水平方向上受绳的拉力和摩擦力,想用让砂和砂桶总质量重力表示小车受到的合外力,首先需要平衡摩擦力;其次:设小车加速度为a,则:绳上的力为F=Ma,对让砂和砂桶总质量来说:mg-Ma=ma,即:mg=(M+m)a,如果用让砂和砂桶总质量的重力表示小车受到的合外力,则Ma=(M+m)a,必须要满足让砂和砂桶总质量远小于小车的总质量;
(3)纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
解答 解:(1)平衡摩擦力时,将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动,以使小车的重力沿斜面分力和摩擦力抵消,那么小车的合力就是绳子的拉力,可以根据纸带上打的点迹是否均匀来判断是否做匀速运动,故该同学平衡摩擦力的方法是错误的;
(2)根据牛顿第二定律得,a=$\frac{mg}{M+m}$.
绳子的拉力为滑块的合力为T=Ma=$\frac{Mmg}{M+m}=\frac{mg}{1+\frac{m}{M}}$.当m<<M时,砂和砂桶的重力等于滑块所受合外力.
(3)解:利用匀变速直线运动的推论得:
vA=$\frac{{s}_{3}+{s}_{4}}{2T}=\frac{0.0833+0.0895}{0.2}$=0.86m/s.
由于相邻的计数点间的位移之差不等,故采用逐差法求解加速度.
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:s4-s1=3a1T2
s5-s2=3a2T2
s6-s3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值
得:a=$\frac{1}{3}$(a1+a2+a3)
带入数据解得:a=0.64m/s2
故答案为:(1)错;(2)远小于;(3)0.86,0.64
点评 实验问题需要结合物理规律去解决.本实验只有在满足平衡摩擦力和小车质量远大于钩码质量的双重条件下,才能用砂和砂桶重力代替小车所受的合力,要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 如图所示,放在水平桌面上的木块A处于静止状态,所挂的砝码和托盘的总质量为0.6kg,弹簧测力计读数为2N,滑轮摩擦不计,若轻轻取走盘中的部分砝码,使总质量减小到0.3kg,将会出现的情况是(取g=10m/s2)( )
如图所示,放在水平桌面上的木块A处于静止状态,所挂的砝码和托盘的总质量为0.6kg,弹簧测力计读数为2N,滑轮摩擦不计,若轻轻取走盘中的部分砝码,使总质量减小到0.3kg,将会出现的情况是(取g=10m/s2)( )| A. | 弹簧测力计的读数将变小 | B. | A将向左运动 | ||
| C. | A所受的摩擦力将减小3 N | D. | A所受的合力将要变大 |
 如图,物体在水平力F作用下静止于粗糙斜面上.若稍许增大F,仍使物体静止在斜面上,则斜面对物体的静摩擦力Ff、支持力FN以及这两个力(Ff和FN)的合力F合变化情况是( )
如图,物体在水平力F作用下静止于粗糙斜面上.若稍许增大F,仍使物体静止在斜面上,则斜面对物体的静摩擦力Ff、支持力FN以及这两个力(Ff和FN)的合力F合变化情况是( )| A. | Ff不一定增大,FN一定增大,F合一定增大 | |
| B. | Ff一定增大,FN一定增大,F合不变 | |
| C. | Ff、FN不一定增大,F合一定增大 | |
| D. | Ff、FN、F合均增大 |
 如图,均匀杆AB重为G,A端用细绳吊着,在B端施加一个水平拉力F,使AB静止,此时细绳拉力为T,与竖直方向成β角,AB杆与水平成α角,下列说法正确的是( )
如图,均匀杆AB重为G,A端用细绳吊着,在B端施加一个水平拉力F,使AB静止,此时细绳拉力为T,与竖直方向成β角,AB杆与水平成α角,下列说法正确的是( )| A. | T≤F | B. | β≥0° | C. | (α+β)<90° | D. | T的大小与F无关 |
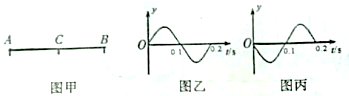
| A. | 两列波在A、B间的传播速度均为20m/s | |
| B. | 两列波的波长都是1m | |
| C. | 在t2=0.9s时刻,A处质点经过平衡位置且振动方向向上 | |
| D. | 在两列波相遇的过程中,C点为振动始终加强 |

| I/A | 0.06 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| U/V | 2.54 | 2.50 | 2.39 | 2.38 | 2.20 | 2.10 |
(2)若将方框内的电路等效成电动势为E、内电阻为r的电源,根据图象求出等小电源的电动势E=2.6V,等效电源的内电阻r=1.0Ω;
(3)若电流表内阻为0,当滑动变阻器的滑片移至最上端时,电流表示数是2.6A;
(4)滑动变阻器滑片移动过程中,滑动变阻器的最大功率是1.69W.
 如图所示,带正电的绝缘小滑块A,被长R=0.4m的绝缘细绳竖直悬挂,悬点O距水平地面的高度为3R;小滑块B不带电.位于O点正下方的地面上.长L=2R的绝缘水平传送带上表面距地面的高度h=2R,其左端与O点在同一竖直线上,右端的右侧空间有方向竖直向下的匀强电场.在.点与传送带之间有位置可调的固定钉子(图中未画出),当把A拉到水平位置由静止释放后,因钉子阻挡,细绳总会断裂,使得A能滑上传送带继续运动,若传送带逆时针匀速转动,A刚好能运动到传送带的右端.已知绝缘细绳能承受的最大拉力是A重力的5倍,A所受电场力大小与重力相等,重力加速度g=10m/s2,A、B均可视为质点,皮带传动轮半径很小,A不会因绳断裂而损失能量、也不会因摩擦而损失电荷量.
如图所示,带正电的绝缘小滑块A,被长R=0.4m的绝缘细绳竖直悬挂,悬点O距水平地面的高度为3R;小滑块B不带电.位于O点正下方的地面上.长L=2R的绝缘水平传送带上表面距地面的高度h=2R,其左端与O点在同一竖直线上,右端的右侧空间有方向竖直向下的匀强电场.在.点与传送带之间有位置可调的固定钉子(图中未画出),当把A拉到水平位置由静止释放后,因钉子阻挡,细绳总会断裂,使得A能滑上传送带继续运动,若传送带逆时针匀速转动,A刚好能运动到传送带的右端.已知绝缘细绳能承受的最大拉力是A重力的5倍,A所受电场力大小与重力相等,重力加速度g=10m/s2,A、B均可视为质点,皮带传动轮半径很小,A不会因绳断裂而损失能量、也不会因摩擦而损失电荷量. 如图所示,固定于水平桌面上的金属框架edcf,处于竖直向下的匀强磁场中,金属棒ab在框架上可无摩擦滑动,此时abcd构成一个边长为L的正方形,棒的电阻为r,其余部分电阻不计,开始时磁感应强度为B0.
如图所示,固定于水平桌面上的金属框架edcf,处于竖直向下的匀强磁场中,金属棒ab在框架上可无摩擦滑动,此时abcd构成一个边长为L的正方形,棒的电阻为r,其余部分电阻不计,开始时磁感应强度为B0.