题目内容
(10分)特种兵过山谷的一种方法可简化为如图所示的模型:将一根长不可伸长的细绳的两端固定在相距为d的A、B两等髙处,细绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP沿竖直方向,且大小等于 d。(不计滑轮与绳的质量,不计滑轮的大小及摩擦,重力加速度为g)若甲对滑轮的拉力沿水平方向,求拉力的大小。
d。(不计滑轮与绳的质量,不计滑轮的大小及摩擦,重力加速度为g)若甲对滑轮的拉力沿水平方向,求拉力的大小。
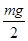
解析试题分析:设绳中的张力为 T,BP 绳与竖直方向间的夹角为θ。
由已知条件可知 :sinθ=0.8,cosθ= 0.6(2分)
由初始状态滑轮的受力情况和共点力作用下的平衡条件可知:
在竖直方向:T + Tcosθ = mg (3分)
在水平方向: Tsinθ=" F" (3分)
联立解得F = 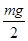 (2分)
(2分)
考点:本题考查力的平衡和正交分解法。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 ,网兜的质量不计.
,网兜的质量不计.
 ,球的重力大小为G,竖直挡板对球的压力大小为
,球的重力大小为G,竖直挡板对球的压力大小为 ,各处的摩擦都不计,试回答下列问题:
,各处的摩擦都不计,试回答下列问题:
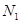 和桌面对圆柱体支持力
和桌面对圆柱体支持力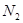 的大小.
的大小.






