题目内容
14.甲、乙同学在平直跑道上玩追逐游戏.开始时甲静止在乙的前方,某时刻,乙以6m/s的速度从甲的身边跑过,从乙在甲身边经过时算起,经过0.5s的反应时间甲开始追赶乙.若乙作匀速运动,甲先以4m/s2的加速度作匀加速运动,达到最大速度8m/s后作匀速运动.求:(1)甲追上乙前两人的最大距离是多少?
(2)甲一共要追逐多长时间才能追上乙?
(3)若甲的最大速度不变,要求甲在起跑后4.5s内追上乙,则甲应先以多大的加速度加速?
分析 (1)当两人的速度相等时距离最大,由速度公式求时间,再由位移公式求解最大距离.
(2)甲追上乙时两者的位移相等,由位移关系和位移公式结合解答.
(3)与上题相似,由位移关系和位移公式结合求解.
解答 解(1)当两人的速度相等时距离最大,设甲经过时间t时两者距离最大,由 v乙=at得:
t=$\frac{{v}_{乙}^{\;}}{a}$=$\frac{6}{4}$=1.5s
最大距离是 S=v乙(t+0.5)-$\frac{1}{2}a{t}^{2}$=6×2-$\frac{1}{2}$×4×1.52=7.5m
(2)当甲的速度到达最大时通过的位移 x甲=$\frac{{v}_{甲}^{2}}{2a}$=$\frac{{8}^{2}}{2×4}$m=8m
所用时间 t1=$\frac{{v}_{甲}}{a}$=$\frac{8}{4}$s=2s
此过程中乙的位移 x乙=v乙(t1+0.5)=6×2.5m=15m
可知甲的速度刚达最大时还没有追上乙,设再经过时间t2,甲追上乙
则有 x乙-x甲=v甲t2-v乙t2,得 t2=3.5s
共用时 t总=t1+t2=5.5s
(3)设甲应先以加速度a′加速,才能满足要求.
则 v乙(t3+0.5)=$\frac{{v}_{甲}^{2}}{2a′}$+v甲(t3-$\frac{{v}_{甲}}{a′}$)
解得 a′=$\frac{16}{3}$m/s2.
答:
(1)甲追上乙前两人的最大距离是7.5m.
(2)甲一共要追逐5.5s时间才能追上乙.
(3)若甲的最大速度不变,要求甲在起跑后4.5s内追上乙,则甲应先以大小为$\frac{16}{3}$m/s2的加速度加速.
点评 解决本题的关键理清运动过程,分析两个运动员之间的关系,如位移关系、时间关系,再运用运动学公式灵活求解.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案| A. | 甲车超前,乙车落后 | B. | 乙车超前,甲车落后 | ||
| C. | 他们仍齐头并进 | D. | 甲车先超前于乙车,后落后于乙车 |
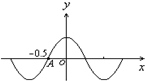 一列波沿直线传播,在某一时刻的波形图如图所示,质点A的位置与坐标原点相距0.5m,此时质点A沿y轴正方向运动,再经过0.02s将第一次达到最大位移,由此可见( )
一列波沿直线传播,在某一时刻的波形图如图所示,质点A的位置与坐标原点相距0.5m,此时质点A沿y轴正方向运动,再经过0.02s将第一次达到最大位移,由此可见( )| A. | 这列波波长是1.0m | |
| B. | 这列波频率是50Hz | |
| C. | 这列波波速是25m/s | |
| D. | 这列波的传播方向是沿x轴的负方向 |
| A. | 机械波在介质中的传播速度仅由介质决定,与机械波的频率无关;电磁波在介质中的传播速度不仅取决于介质,还与电磁波的频率有关 | |
| B. | 用激光“焊接”剥落的视网膜利用了激光的相干性好 | |
| C. | 黄光、蓝光分别通过同一干涉装置形成的干涉条纹,其中黄光产生的干涉条纹较宽 | |
| D. | 光从光疏介质射向光密介质有可能发生全反射 |
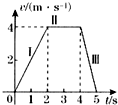 如图所示,物体的运动分三段,第1、2s为第I段,第3、4s为第II段,第5s为第III段,则下列说法正确的是( )
如图所示,物体的运动分三段,第1、2s为第I段,第3、4s为第II段,第5s为第III段,则下列说法正确的是( )| A. | 第1s内与第5s内的速度方向相反 | |
| B. | 第1s的加速度小于第5s的加速度 | |
| C. | 第I段与第III段的平均速度相等 | |
| D. | 第I段与第III段的加速度和速度的方向都相同 |

| A. | 物块处于平衡状态 | |
| B. | 物块受四个力作用 | |
| C. | 在角速度一定时,物块到转轴的距离越远,物块越容易脱离圆盘 | |
| D. | 在物块到转轴距离一定时,物块运动周期越小,越容易脱离圆盘 |
 某电荷形成的电场的电场线中的A、B两点,检验电荷在电场中的运动轨迹为图中虚线所示,关于检验电荷的说法正确是( )
某电荷形成的电场的电场线中的A、B两点,检验电荷在电场中的运动轨迹为图中虚线所示,关于检验电荷的说法正确是( )| A. | 检验电荷带负电 | |
| B. | 检验电荷的电势能一定减小,动能一定增大 | |
| C. | 检验电荷的电势能一定增大,动能一定减小 | |
| D. | 由B到A,检验电荷的动能一定增加 |
