题目内容
【题目】如图所示,足够长的光滑平行金属导轨MN、PQ水平放置,导轨间距为L,一个磁感应强度B的匀强磁场垂直穿过导轨平面向下,导轨的上端M与P间接有电容为C的电容器,金属棒开始静止.对金属棒施加一个水平向右、大小为F的恒力作用,不计一切摩擦,一切电阻都不计,则经过时间t的过程中( )
A.金属棒可能做变加速运动
B.金属棒中的电流恒定
C.电容器所带电荷量 ![]()
D.电容器储存的电场能为 ![]()
【答案】B,C,D
【解析】解:A、经过时间△t时,金属棒速度设为v,根据动量定理可得:F△t﹣BIL△t=mv﹣0,金属棒切割磁感线产生电动势变化△E=BL△v,通过电容器的电量Q=I△t=CBLv,
所以有F△t﹣BLCBLv=mv﹣0,解得:v= ![]() ,又加速度定义式a=
,又加速度定义式a= ![]() ,可得加速度a=
,可得加速度a= ![]() ,为定值,A不符合题意;
,为定值,A不符合题意;
B、对金属棒,应用牛顿第二定律有F﹣BIL=ma,由于加速度、拉力F恒定,所以安培力恒定,电流强度恒定,B符合题意;
C、电流强度I=CBLa= ![]() ,经过时间t流过电路横截面的电量Q=It=
,经过时间t流过电路横截面的电量Q=It= ![]() ,C符合题意;
,C符合题意;
D、电容器所带的电荷量与电容器两端电压关系图象如图所示,
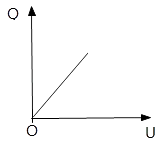
图象与坐标轴围成的面积表示电容器储存的电能,所以电容器储存的电场能为E= ![]() =
= ![]() =
= ![]() =
= ![]() ,D符合题意;
,D符合题意;
故答案为:BCD.
本题主要从电路知识考查电磁感应,首先根据右手定则判断感应电动势的大小,结合闭合电路欧姆定律以及动量定理,求解即可。

练习册系列答案
相关题目