Question

【题目】如图所示，质量为mB=14kg的木板B放在水平地面上，质量为mA=10kg的木箱A放在木板B上．一根轻绳一端拴在木箱上，另一端拴在地面的木桩上，绳绷紧时与水平面的夹角为θ=37°．已知木箱A与木板B之间的动摩擦因数μ1=0.5，木板B与地面之间的动摩擦因数μ2=0.4．重力加速度g取10m/s2 ． 现用水平力F将木板B从木箱A下面匀速抽出，试求：（sin37°=0.6，cos37°=0.8）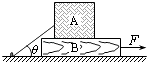

（1）绳上张力T的大小；
（2）拉力F的大小．

Answer 1

【答案】
（1）解：对物体A受力分析及建立直角坐标系，如图所示：

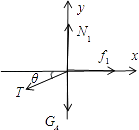
∵A静止，受力平衡

∴在x轴上：

Tcosθ=f1…①

在y轴上：

N1=Tsinθ+mAg…②

又∵f1=μ1 N1…③

∴由①②③得：

T=100 N

即绳上张力T的大小为100N．

答：绳上张力T的大小为100N．

（2）解：对物体B受力分析及建立直角坐标系，如图所示：

∵B静止，受力平衡

∴在x轴上：

F=f1+f2…④

在y轴上：

N2=N1+mBg…⑤

又∵f2=μ2N2…⑥

∴由④⑤⑥得：

F=200 N

即拉力F的大小为200N．

答：拉力F的大小为200N．

【解析】（1）对木块A受力分析，受到重力、支持力、B对A的摩擦力和细线的拉力，根据共点力平衡条件列式求解即可；（2）对木块B受力分析，受到重力、A对B的压力和摩擦力、地面的支持力和摩擦力，最后根据共点力平衡条件列式求解即可．