题目内容
12.我国先后发射的“嫦娥一号”和“嫦娥二号”探月卫星,“嫦娥二号”卫星离月球表面更近.假设“嫦娥二号”卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的$\frac{1}{81}$,月球的半径约为地球半径的$\frac{1}{4}$,地球上的第一宇宙速度约为7.9km/s,则该探月卫星绕月运行的速率约为多少?分析 第一宇宙速度是近地卫星的环绕速度.
探月卫星贴近月球表面,运行的速率即为月球的第一宇宙速度.
根据月球质量和地球质量的关系,月球半径和地球半径的关系,根据第一宇宙速度的表达式求出月球的第一宇宙速度和地球第一宇宙速度的关系,从而求出月球的第一宇宙速度大小
解答 解:设地球的质量为m1,月球的质量为m2,地球半径为R1,月球半径为R2.
对于近地卫星,由G$\frac{{m}_{1}m}{{R}_{1}^{2}}$=m$\frac{{v}_{1}^{2}}{{R}_{1}}$
得卫星绕地运行的速率v1=$\sqrt{\frac{G{m}_{1}}{{R}_{1}}}$
其中v1=7.9 km/s
同理卫星绕月运行的速率v2=$\sqrt{\frac{G{m}_{2}}{{R}_{2}}}$
联立解得v2=1.8 km/s.
答:该探月卫星绕月运行的速率约为1.8 km/s.
点评 要求解一个物理量大小,我们应该把这个物理量先表示出来,再根据已知量进行求解.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
相关题目
2.在众多围绕地球做匀速圆周运动的人造地球卫星中,卫星轨道半径越小的,下述判断正确的是( )
| A. | 周期越小 | B. | 线速度越小 | C. | 角速度越小 | D. | 加速度越大 |
3.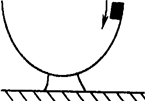 质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )
质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )
 质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )
质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的使用使得木块的速率不变,如图所示,那么( )| A. | 因为速率不变,所以木块的加速度为零 | |
| B. | 木块下滑过程中所受的合外力越来越大 | |
| C. | 木块下滑过程中所受的摩擦大小不变 | |
| D. | 木块下滑过程中的加速度大小不变,方向始终指向球心 |
20. 如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,小球处于静止状态,小球所带电荷量为q,细丝悬线与竖直方向的夹角为θ,则( )
如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,小球处于静止状态,小球所带电荷量为q,细丝悬线与竖直方向的夹角为θ,则( )
 如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,小球处于静止状态,小球所带电荷量为q,细丝悬线与竖直方向的夹角为θ,则( )
如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,小球处于静止状态,小球所带电荷量为q,细丝悬线与竖直方向的夹角为θ,则( )| A. | 小球所带电荷为负电荷 | |
| B. | 小球受到重力、悬线的拉力以及静电力 | |
| C. | 小球所带电荷受到的静电力方向与电场强度方向相反 | |
| D. | 若剪断悬线,则小球沿着水平方向做匀加速直线运动 |
9.下列物理量中,属于矢量的是( )
| A. | 时间 | B. | 时间 | C. | 位移 | D. | 时间 |
 如图所示,两竖直放置的平行光滑导轨处于垂直于导轨平面的匀强磁场中,金属杆ab可沿导轨滑动,金属杆ab始终与导轨接触良好且保持水平,原先S断开,让ab杆由静止下滑,一段时间后闭合S,则从S闭合开始记时,ab杆的运动速度v随时间t的关系图不可能是下图中的哪一个?( )
如图所示,两竖直放置的平行光滑导轨处于垂直于导轨平面的匀强磁场中,金属杆ab可沿导轨滑动,金属杆ab始终与导轨接触良好且保持水平,原先S断开,让ab杆由静止下滑,一段时间后闭合S,则从S闭合开始记时,ab杆的运动速度v随时间t的关系图不可能是下图中的哪一个?( )



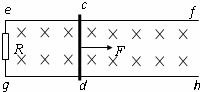 如图,ef,gh为水平放置的足够长的平行光滑导轨,导轨间距为L=1m,导轨左端连接一个R=2Ω的电阻,将一根质量为0.2kg的金属棒cd垂直地放置导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直于导轨平面向下.现对金属棒施加一水平向右的拉力F,且保持拉力的功率恒为P=18W,使棒从静止开始向右运动.
如图,ef,gh为水平放置的足够长的平行光滑导轨,导轨间距为L=1m,导轨左端连接一个R=2Ω的电阻,将一根质量为0.2kg的金属棒cd垂直地放置导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直于导轨平面向下.现对金属棒施加一水平向右的拉力F,且保持拉力的功率恒为P=18W,使棒从静止开始向右运动. 如图所示,一根长为l的细线,一端固定在顶板上,另一端栓一个质量为m的小球,现使细线偏离竖直方向α=60°角后,从A点处无初速地释放小球,试问:
如图所示,一根长为l的细线,一端固定在顶板上,另一端栓一个质量为m的小球,现使细线偏离竖直方向α=60°角后,从A点处无初速地释放小球,试问: