��Ŀ����
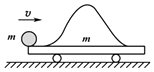
����Ŀ����ͼ����ʾ������Ϊm=1kg��С�����ڳ�ֱˮƽ���ϣ���ˮƽϸ�߽����ڰ뾶ΪR=0.2m�ı���ԲͲ�ϣ�t=0ʱ�̣�ԲͲ�ڵ綯���������ɾ�ֹ��ʼ����ֱ������ת����С����v��tͼ����ͼ�ң����͵���֮��Ķ�Ħ������Ϊ��=0.2��������ϸ����ԲͲ�ϲ��Ƶĺ�ȣ��� ��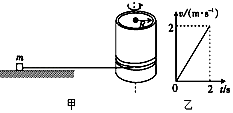
A.ԲͲת���Ľ��ٶ������=5t
B.ϸ�ߵ�������СΪ2 N
C.ϸ��������˲ʱ��������P=4t
D.��0��2 s�ڣ�ϸ����С������Ĺ�Ϊ6J
���𰸡�A,D
���������⣺A��С�����ٶ�v=t��m/s������ԲͲ��Ե�����ٶ�Ϊv=t��m/s������ô�����ٶ� ![]() ����A��ȷ��
����A��ȷ��
B��С���ļ��ٶ�a=1m/s2������ţ�ٵڶ����ɿɵã�F����mg=ma�����ԣ�F=ma+��mg=3N����B����
C��ϸ��������˲ʱ����P=Fv=3t��W������C����
D����0��2 s�ڣ�С����λ�� ![]() ����ϸ����С������Ĺ�W=Fs=6J����D��ȷ��
����ϸ����С������Ĺ�W=Fs=6J����D��ȷ��
��ѡ��AD��
�����㾫����������Ĺؼ���������������������֪ʶ�����պ����Ĺ��ɸ���W=F��S��cos�Ƚ��м��㣬����ʽֻ�����ں����������Լ��Թ��ʵļ�������������⣬�˽�ʵļ��㣺 P = W/tW ��ʾ������λ�ǽ���J��. t��ʾʱ�� ����λ���루s�� P��ʾ���ʣ���λ�����أ�W��1 W= 1 J/s��