题目内容
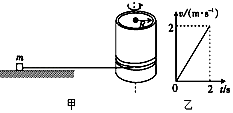
【题目】如图所示的装置叫做阿特伍德机，是阿特伍德创制的一种著名力学实验装置．绳子两端的物体下落（上升）的加速度总是小于自由落体的加速度g，同自由落体相比，下落相同的高度，所花费的时间要长，这使得实验者有足够的时间从容的观测、研究．已知物体A、B的质量相等均为M，物体C的质量为m，轻绳与轻滑轮间的摩擦不计，轻绳不可伸长且足够长，如果m= 
M，将BC由静止释放，下落距离为H，此时A未与滑轮接触，求：
（1）此时A的速度大小；
（2）此过程中B对C做的功．
【答案】
（1）解：对整体由动能定律可得：
（M+m）gH﹣MgH= 
v= 
= 
答：此时A的速度大小
（2）解：对C由动能定理得：
mgH﹣W= 
W= 
= 
答：此过程中B对C做的功﹣
【解析】（1）通过整体由动能定理即可求的速度；（2）对C由动能定理即可求的B对C做功
【考点精析】认真审题，首先需要了解动能定理的综合应用(应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷)．
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案【题目】科学探究活动通常包括以下环节：提出问题，作出假设，制定计划，搜集证据，评估交流等．一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下
A．有同学认为：运动物体所受空气阻力可能与其运动速度有关
B．他们计划利用一些“小纸杯”作为研究对象，用超声测距仪等仪器测量“小纸杯”在空中直线下落时的下落距离、速度随时间变化的规律，以验证假设
C．在相同的实验条件下，同学们首先测量了单只“小纸杯”在空中下落过程中不同时刻的下落距离，将数据填入表中，如图（a）是对应的位移—时间图线．然后将不同数量的“小纸杯”叠放在一起从空中下落，分别测出它们的速度—时间图线，如图（b）中图线1、2、3、4、5所示
D.同学们对实验数据进行分析、归纳后，证实了他们的假设．
回答下列提问：
（1）与上述过程中A、C步骤相应的科学探究环节分别是________、________；
（2）图（a）中的AB段反映了运动物体在做________运动，表中x处的值为________；
（3）图（b）中各条图线具有共同特点，“小纸杯”在下落的开始阶段做__________运动，最后“小纸杯”做________运动；
时间（s） | 下落距离（m） |
0.0 | 0.000 |
0.4 | 0.036 |
0.8 | 0.469 |
1.2 | 0.957 |
1.6 | 1.447 |
2.0 | x |
