题目内容
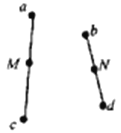
【题目】如图所示,比荷为![]() 的电子以大小不同的初速度沿AB边射入边长为a的等边三角形的匀强磁场区域中,磁感应强度大小为B,(不计重力作用)则:
的电子以大小不同的初速度沿AB边射入边长为a的等边三角形的匀强磁场区域中,磁感应强度大小为B,(不计重力作用)则:
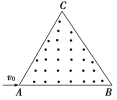
(1)若电子从AC边射出磁场区域,求电子在磁场中的运动时间t;
(2)若要电子从BC边射出,求入射速度大小的范围;
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)电子进入磁场后受到洛伦兹力作用而做匀速圆周运动, 利用轨迹从直边界进出具有对称性求圆心角从而确定时间.
(2)电子能经过BC边恰好从C点离开时,轨迹半径最小,由几何知识求出最小的半径,由半径公式求出初速度的最小值,即可得到初速度的范围.
(1)由洛伦兹力提供向心力,可得![]()
可得:![]()
而![]() ,可知
,可知![]()
当电子从AC边离开磁场时,根据直边界的对称性可知弦切角为60°,则圆心角为120°
则运动时间为![]()
联立得:![]()
(2)当电子从C点离开磁场时,是电子做匀速圆周运动从BC边离开的临界情况,如图所示:
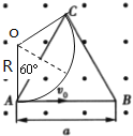
则由几何知识:![]() ,可得
,可得![]()
联立得![]()
速度越大半径越大,则要从BC边飞离的磁感应强度的取值范围为![]() .
.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目