题目内容
【题目】如图所示，在xoy平面第一象限整个区域分布匀强电场，电场方向平行于y轴向下，在第四象限内存在匀强磁场，磁场方向垂直纸面向外。质量为m、带电量为+q的粒子从y轴上P点以初速度v0垂直y轴射入匀强电场，在电场力作用下从x轴上Q点以与x轴正方向成45°角进入匀强磁场。已知OQ=d，不计粒子重力。求：
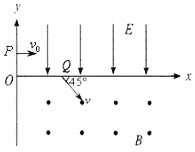
(1)P点的坐标；
(2)要使粒子能再次进入电场，求磁感应强度B的取值范围；（结果可保留根号）
【答案】（1）
（2）
【解析】
(1)粒子在第一象限内做类平抛运动，在x轴方向上做匀速直线运动，在y轴方向做初速度为零的匀加速直线运动，已知在Q点时的速度方向为45°，可知此时沿两个坐标轴的速度都是v0，在x轴和y轴方向分别列式，可求出OP的距离，从而得到P点的坐标；
(2) 对粒子在第四象限中的运动轨道进行分析，找到临界状态，即轨道恰好与y轴相切为轨道的最大半径，结合洛伦兹力做向心力的公式可求出此时的磁感应强度，该磁感应强度为最小值，从而可表示出磁感应强度的范围。
(1)设粒子进入电场时y方向的速度为vy，则
粒子在电场中做类平抛运动，设粒子在电场中运动时间为t，
在水平方向：
，在竖直方向：
解得：
，P点坐标为：（0，0.5d）；
(2)粒子刚好能再进入电场的轨迹如图所示，设此时的轨迹半径为r1，
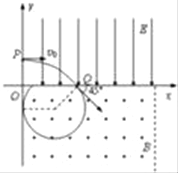
由数学知识得：
解得：
粒子在磁场中运动的速度
由牛顿第二定律得
解得：
要使粒子能再进入电场，磁感应强度B的范围为
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某同学在“探究小车速度随时间变化的规律”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出0、1、2、3、4、5、6共7个测量点。其相邻点间的距离如图所示，每两个相邻的测量点之间的时间间隔为0.10，试完成下面问题。
（1）根据纸带上各个测量点间的距离，某同学已将1、2、3、5点对应的时刻的瞬时速度进行计算并填入表中，请你将4点对应的时刻的瞬时速度填入表中。（要求保留3位有效数字）
瞬时速度 | v1 | v2 | v3 | v4 | v5 |
数值（m·s-1） | 0.165 | 0.214 | 0.263 | ________ | 0.363 |
（2）在图中所示的直角坐标系中画出小车的瞬时速度随时间变化的关系图线________。
（3）由图象求出小车的加速度a=________ m/s2。
