题目内容
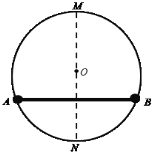
【题目】如图所示，半径为 R 的光滑圆环竖直放置，直径 MN 为竖直方向，环上套有两个小球 A 和 B， A、 B 之间用一长为
R 的轻杆相连，小球可以沿环自由滑动，开始时杆处于水平状态，已知 A 的质量为 m， 重力加速度为 g。
（1）若 B 球质量也为 m，求开始时杆对 B 球的弹力大小；
（2）若 B 的质量为 3m，由静止释放轻杆，求 B 球由初始位置到达N 点的过程中，轻杆对 B 球所做的功。
【答案】（1）
（2）
mgR
【解析】
(1)对B球受力分析，受重力、支持力和杆的弹力，根据平衡条件并结合合成法列式求解即可．(2)两球组成的系统机械能守恒，由系统的机械能守恒和两球速率相等的关系列式，即可求出B到达N点的速度，再运用动能定理求解功．
(1)设杆对B的弹力大小为N1，B球的受力分析如下图所示:
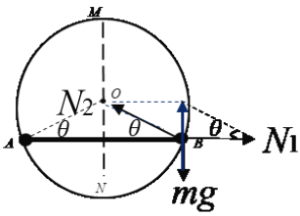
由图可知：
解得：
= 30°
而：
解得:
(2)设B球到达N点时A、B的速率分别为vA、vB，由下图中的几何关系可知，
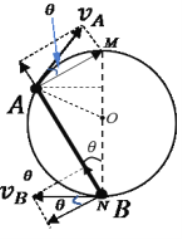
球A上升高度为:
解得：h1=R
球B下降高度：
对系统由机械能守恒定律得：
又有：
对B球的运动过程，由动能定理：
联立以上各式得：W =mgR
练习册系列答案
相关题目
