题目内容
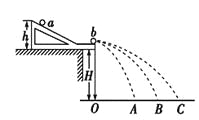
【题目】(1)动量定理可以表示为Δp=FΔt,其中动量p和力F都是矢量。在运用动量定理处理二维问题时,可以在相互垂直的x、y两个方向上分别研究。例如,质量为m的小球斜射到木板上,入射的角度是θ,碰撞后弹出的角度也是θ,碰撞前后的速度大小都是v,如图1所示。碰撞过程中忽略小球所受重力。

a.分别求出碰撞前后x、y方向小球的动量变化Δpx、Δpy;
b.分析说明小球对木板的作用力的方向。
(2)激光束可以看作是粒子流,其中的粒子以相同的动量沿光传播方向运动。激光照射到物体上,在发生反射、折射和吸收现象的同时,也会对物体产生作用。光镊效应就是一个实例,激光束可以像镊子一样抓住细胞等微小颗粒。
一束激光经S点后被分成若干细光束,若不考虑光的反射和吸收,其中光束①和②穿过介质小球的光路如图②所示。图中O点是介质小球的球心,入射时光束①和②与SO的夹角均为θ,出射时光束均与SO平行。请在下面两种情况下,分析说明两光束因折射对小球产生的合力的方向。
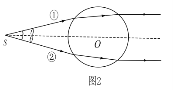
a.光束①和②强度相同;
b.光束①比②强度大。
【答案】(1)a.![]() ,
,![]() ,方向沿y轴正方向b.沿y轴负方向(2)a.两光束对小球的合力的方向沿SO向左b.两光束对小球的合力的方向指向左上方
,方向沿y轴正方向b.沿y轴负方向(2)a.两光束对小球的合力的方向沿SO向左b.两光束对小球的合力的方向指向左上方
【解析】(1)a.x方向:
动量变化为![]()
y方向:动量变化为![]()
方向沿y轴正方向
b.根据动量定理可知,木板对小球作用力的方向沿y轴正方向;根据牛顿第三定律可知小球对木板作用力的方向沿y轴负方向
(2)a.仅考虑光的折射,设![]() 时间内没每束光穿过小球的粒子数为n,每个粒子动量的大小为p。
时间内没每束光穿过小球的粒子数为n,每个粒子动量的大小为p。
这些粒子进入小球前的总动量为![]()
从小球出射时的总动量为![]()
![]() 、
、![]() 的方向均沿SO向右
的方向均沿SO向右
根据动量定理![]()
可知,小球对这些粒子的作用力F的方向沿SO向右;根据牛顿第三定律,两光束对小球的合力的方向沿SO向左。
b.建立如图所示的Oxy直角坐标系
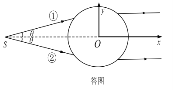
x方向:根据(2)a同理可知,两光束对小球的作用力沿x轴负方向。
y方向:设![]() 时间内,光束①穿过小球的粒子数为
时间内,光束①穿过小球的粒子数为![]() ,光束②穿过小球的粒子数为
,光束②穿过小球的粒子数为![]() ,
,![]() 。
。
这些粒子进入小球前的总动量为![]()
从小球出射时的总动量为![]()
根据动量定理:![]()
可知,小球对这些粒子的作用力![]() 的方向沿y轴负方向,根据牛顿第三定律,两光束对小球的作用力沿y轴正方向。所以两光束对小球的合力的方向指向左上方。
的方向沿y轴负方向,根据牛顿第三定律,两光束对小球的作用力沿y轴正方向。所以两光束对小球的合力的方向指向左上方。

【题目】地球和火星绕太阳公转可视为匀速圆周运动,忽略行星自转影响。根据下表,火星和地球相比( )
行星 | 星体半径/m | 星体质量/kg | 公转轨道半径/m |
地球 | 6.4×106 | 6.0×1024 | 1.5×1011 |
火星 | 3.4×106 | 6.4×1023 | 2.3×1011 |
A.火星的公转周期较大
B.火星公转的向心加速度较大
C.火星表面的重力加速度较小
D.火星的第一宇宙速度较大