题目内容
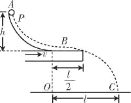
【题目】如图所示,两个正三棱柱A、B紧靠着静止于水平地面上,三棱柱的中间有一个半径为R的光滑圆柱C,C的质量为2m,A、B的质量均为m.A、B与地面的动摩擦因数为μ.设最大静摩擦力等于滑动摩擦力,重力加速度为g.
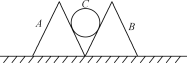
(1) 三者均静止时A对C的支持力为多大?
(2) A、B若能保持不动,μ应该满足什么条件?
(3) 若C受到经过其轴线竖直向下的外力而缓慢下降到地面,求该过程中摩擦力对A做的功.
【答案】(1) FN=2mg. (2)μ≥![]() . (3)-
. (3)-![]() .
.
【解析】
(1)对C进行受力分析,根据平衡求解A对C的支持力;
(2)A保持静止,则地面对A的最大静摩擦力要大于等于C对A的压力在水平方向的分力,据此求得动摩擦因数μ应该满足的条件;
(3)C缓慢下落同时A、B也缓慢且对称地向左右分开,A受力平衡,根据平衡条件求解滑动摩擦力大小,根据几何关系得到A运动的位移,再根据功的计算公式求解摩擦力做的功。
(1) C受力平衡,2FNcos60°=2mg
解得FN=2mg
(2) 如图所示,A受力平衡F地=FNcos60°+mg=2mg
f=FNsin60°=![]() mg
mg
因为f≤μF地,所以μ≥![]()
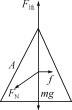
(3) C缓慢下降的同时A、B也缓慢且对称地向左右分开.A的受力依然为4个,如图所图,但除了重力之外的其他力的大小发生改变,f也成了滑动摩擦力.
A受力平衡知F′地=F′Ncos60°+mg
f′=F′Nsin60°=μF′地
解得f′=![]()
即要求![]() -μ>0,与本题第(2)问不矛盾.
-μ>0,与本题第(2)问不矛盾.
由几何关系知:当C下落地地面时,A向左移动的水平距离为x=![]() R
R
所以摩擦力的功W=-f′x=-![]()

练习册系列答案
相关题目