题目内容
【题目】如图所示为弹簧弹射装置，在内壁光滑、水平固定的金属管中放有轻弹簧，在其两端各放置一个金属小球1和2（两球直径略小于管径且与弹簧不固连），压缩弹簧并锁定．现解除锁定，则两个小球同时沿同一直线向相反方向弹射．按下述步骤进行实验：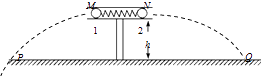
①用天平测出两球质量分别m1、m2；
②用刻度尺测出两管口离地面的高度均为h；
③解除弹簧锁定弹出两球，记录两球在水平地面上的落点P、Q．
回答下列问题：
（1）要测定弹射装置在弹射时所具有的弹性势能，还需测量的物理量有 ． （已知重力加速度g）
A.弹簧的压缩量△x；
B.两球落点P、Q到对应管口M、N的水平距离x1、x2；
C.小球直径；
D.两球从管口弹出到落地的时间t1、t2 ．
（2）根据测量结果，可得弹性势能的表达式为EP= ．
（3）由上述测得的物理量来表示，如果满足关系式 ， 那么说明弹射过程中两小球组成的系统动量守恒．
【答案】
（1）B
（2）
+ 
（3）m1x1=m2x2
【解析】解：（1）由题意可知，弹簧的弹性势能转化为小球的动能，则由EP= 
mv2即可求得弹性势能；故应测量小球的质量m以及通过光电门的速度v，为了测量小球的速度，在做平抛动的水平位移，压缩量以及时间和小球的直径均不需要测量；故B正确，ACD错误．
故选：B；（2）由（1）可知，EP= m1v12+ m2v22
由h= gt2可得：
平抛运动的时间t= 
；
根据水平方向上的匀速直线运动规律可知：
v1= 
；v2= 
即EP= m1v12+ m2v22= + （3）根据动量守恒定律可知，两球碰前动量为零，碰后方向向反，设向左为正，则有：
0=m1v1﹣m2v2
再根据水平方向x=vt可得：
m1x1=m2x2；
所以答案是：（1）B；（2） + ；（3）m1x1=m2x2
