Question

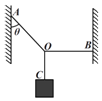
【题目】如图所示，三段不可伸长细绳OA、OB、OC共同悬挂质量为2kg的重物，其中OB是水平的，OA绳与竖直方向的夹角为求

、OB两绳的拉力大小；

若三绳承受的最大拉力相同，逐渐增加C端所挂物体的质量，判断最先断的绳是哪根绳，简单说明理由；

若OA、OB绳所能承受的最大拉力均为l00N，OC绳所能承受的拉力无限大。求：OC绳下端最多能悬挂多重的物体？

Answer 1

【答案】（1）25N、15N；（2）OA先断；（3）80N

【解析】

对物体受力分析可求得：绳OC的拉力

对节点O受力分析如图所示：令OA绳的拉力为F2，OB绳的拉力为F1

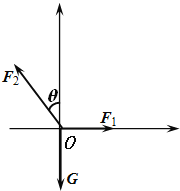
建立直角坐标系如图有：

联立解得：，；故OA绳中的拉力为25N，OB绳中的拉力为15N；

由第一问可知在在悬挂重物的时候OA绳中的拉力最大，因此如果三根绳的承受力一样大，逐渐增加重物的重量OA中的拉力比OB和OC绳中的拉力大，因此OA绳先断；

若OA、OB绳所能承受的最大拉力均为100N，当OB达到100N时，由OA绳中的拉力大于OB绳的拉力可知此时OA绳的拉力超过100N，OA绳已经断，因此应先让OA绳的拉力到达100N，此时OB绳没断；则此时所挂物体的重力为：

所以悬挂物体的重力的最大值。