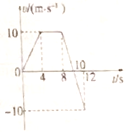
[题目]如图甲所示.ABCD是一长方形有界匀强磁场边界.磁感应强度按图乙规律变化.取垂直纸面向外为磁场的正方向.图中AB＝AD＝L.一质量为m.所带电荷量为q的带正电粒子以速度v0在t＝0时从A点沿AB方向垂直磁场射入.粒子重力不计. (1)若粒子经时间恰好垂直打在CD上.求磁场的磁感应强度B0和粒子运动中的加速度a的大小.(2)若要使粒子恰题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图甲所示，ABCD是一长方形有界匀强磁场边界，磁感应强度按图乙规律变化，取垂直纸面向外为磁场的正方向，图中AB＝AD＝L，一质量为m、所带电荷量为q的带正电粒子以速度v0在t＝0时从A点沿AB方向垂直磁场射入，粒子重力不计。

(1)若粒子经时间恰好垂直打在CD上，求磁场的磁感应强度B0和粒子运动中的加速度a的大小。

(2)若要使粒子恰能沿DC方向通过C点，求磁场的磁感应强度B0的大小及磁场变化的周期T0。

【答案】（1），（2）（n=0,1,2,3，…）；（n=0,1,2,3，…）

【解析】

（1）若粒子经时间t=T0恰好垂直打在CD上，粒子的轨迹必定为3个四分之一圆周，有几何关系定出半径，由洛伦兹力提供向心力，求得磁感应强度B0和运动中的加速度a大小；
（2）若要使粒子恰能沿DC方向通过C点，粒子运动的时间必定为磁感应强度变化的周期的整数倍，根据运动轨迹，结合几何关系求得半径大小，得出磁感应强度B0及变化的周期T0．

（1）若粒子经时间t=T0恰好垂直打在CD上，粒子的轨迹必定为3个四分之一圆周，如图，

由几何关系得，运动半径为r=①
由洛伦兹力提供向心力得，B0qv0＝ ②
联立可得，B0＝ ③
运动中的加速度为：a= ④
由①②③④得，，a=
（2）若要使粒子恰能沿DC方向通过C点，粒子运动的时间必定为磁感应强度变化的周期的整数倍，根据运动的对称性可得，轨道半径r′＝ (n=0、1、2、3、…..)⑤
由由洛伦兹力提供向心力得，B0qv0＝ ⑥
由⑤⑥得，B0＝ (n=0、1、2、3、………)⑦
粒子圆周运动周期为：T= ⑧
磁感应强度变化的周期：T0=T⑨
由⑤⑧⑨得，T0= (n=0、1、2、3、….)

练习册系列答案

A. 沿轨道I运动至P时，需制动减速才能进入轨道Ⅱ

B. 沿轨道Ⅱ运行的周期大于沿轨道I运行的周期

C. 沿轨道Ⅱ运行时，在P点的加速度大于在Q点的加速度

D. 在轨道Ⅱ上由P点运行到Q点的过程中，万有引力对其做正功，它的动能增加，重力势能减小，机械能不变

【题目】如图所示为某同学在一次实验中用打点计时器打出的一条纸带，其中ABCDEF是打点计时器连续打出的6个点，该同学用毫米刻度尺测量A点到各点的距离．并记录在图中（单位：cm，打点计时器工作频率50Hz）则：

（1）图中五个数据中不符合有效数字要求的是_______cm．应改为_______cm．

（2）在纸带上打出D点时的瞬时速度为______m/s，物体运动的加速度为_______m/s2．

【题目】如图所示，一个质量为m，电荷量+q的带电微粒（重力忽略不计），从静止开始经电压加速后，水平进入两平行金属板间的偏转电场中，金属板长L，两板间距d。微粒射出偏转电场时的偏转角θ=30°，接着进入一个方向垂直于纸面向里的匀强磁场区，求：

(1)微粒进入偏转电场时的速度；

(2)两金属板间的电压；

(3)若该匀强磁场的宽度为D，微粒刚好不从磁场右边射出，求该匀强磁场的磁感应强度B。

【题目】【附加题】如图甲所示，间距为d、垂直于纸面的两平行板P、Q间存在匀强磁场。取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示。t=0时刻，一质量为m、带电荷量为+q的粒子（不计重力），以初速度由板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区。当和取某些特定值时，可使时刻入射的粒子经时间恰能垂直打在板上（不考虑粒子反弹）。上述为已知量。