题目内容
8. 如图所示,质量为m的小球系在轻绳的一端,以O为圆心在竖直平面内做半径为R的圆周运动.运动过程中,小球受到空气阻力的作用.设某时刻小球通过圆周的最低点A,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点B,则在此过程中小球克服空气阻力所做的功是( )
如图所示,质量为m的小球系在轻绳的一端,以O为圆心在竖直平面内做半径为R的圆周运动.运动过程中,小球受到空气阻力的作用.设某时刻小球通过圆周的最低点A,此时绳子的拉力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点B,则在此过程中小球克服空气阻力所做的功是( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{3}$mgR | C. | $\frac{1}{2}$mgR | D. | mgR |
分析 小球在轻绳的作用下,在竖直平面内做圆周运动,由最低点的绳子的拉力结合牛顿第二定律可求出此时速度,当小球恰好通过最高点,由此根据向心力与牛顿第二定律可算出速度,最后由动能定理来求出过程中克服阻力做功.
解答 解:小球在最低点A时:
TA=7mg…①
合力提供向心力,故:
TA-mg=m$\frac{{{v}_{A}}^{2}}{R}$…②
小球恰好过最高点B时:
mg=m$\frac{{{v}_{B}}^{2}}{R}$…③
从A到B的过程中,由动能定理得:
-mg•2R-Wf=$\frac{1}{2}$mv2B-$\frac{1}{2}$mv2A…④
解之得:
Wf=$\frac{1}{2}$mgR
故选:C
点评 由绳子的拉力可求出最低点速度,由恰好能通过最高点求出最高点速度,这都是题目中隐含条件.同时在运用动能定理时,明确初动能与末动能,及过程中哪些力做功,做正功还是负功.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一颗烟花弹从地面竖直向上发射,到达的最大高度为20m,不计空气阻力,取重力加速度g=10m/s2,则烟花弹发射的初速度大小为( )
| A. | 5m/s | B. | 10m/s | C. | 20m/s | D. | 40m/s |
3.发现万有引力定律和测出引力常量的科学家分别是( )
| A. | 开普勒、伽利略 | B. | 牛顿、卡文迪许 | C. | 开普勒、卡文迪许 | D. | 牛顿、伽利略 |
20.一质点开始做匀速直线运动,从某时刻起受到一恒力作用.此后,该质点的动能可能( )
| A. | 一直恒定不变 | |
| B. | 先逐渐减小至零,再逐渐增大 | |
| C. | 先逐渐增大至某一最大值,再逐渐减小 | |
| D. | 先逐渐减小至某一非零的最小值,然后不变 |
20.一辆汽车在4s内做匀变速直线运动,初速大小为2m/s,末速大小为10m/s,关于汽车在这段时间内的运动,以下说法可能正确的是( )
| A. | 加速度大小为6m/s2 | B. | 加速度大小为2m/s2 | ||
| C. | 平均速度大小为3m/s | D. | 平均速度大小为6m/s |


 如图所示,一导热性能良好的足够长的汽缸开口向下被吊着,汽缸内的活塞与汽缸内壁紧密接触且可以在缸内无摩擦地自由滑动,大气压强恒为p0,环境温度为T0,活塞重为G,活塞的横截面积为S,此时活塞距汽缸底的距离为d.若在活塞下再吊一重为G1的重物,活塞再次稳定静止时下移的距离为多少?
如图所示,一导热性能良好的足够长的汽缸开口向下被吊着,汽缸内的活塞与汽缸内壁紧密接触且可以在缸内无摩擦地自由滑动,大气压强恒为p0,环境温度为T0,活塞重为G,活塞的横截面积为S,此时活塞距汽缸底的距离为d.若在活塞下再吊一重为G1的重物,活塞再次稳定静止时下移的距离为多少?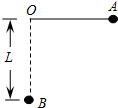 如图8所示,将细线一端系一个质量m=0.5kg的小球,另一端固定于悬点O,小球悬挂起来就是一个摆.现将细线拉直至水平位置OA,从位置A静止释放小球,小球经过悬点O正下方的B点.已知摆长L=0.8m,空气阻力忽略不计,求:
如图8所示,将细线一端系一个质量m=0.5kg的小球,另一端固定于悬点O,小球悬挂起来就是一个摆.现将细线拉直至水平位置OA,从位置A静止释放小球,小球经过悬点O正下方的B点.已知摆长L=0.8m,空气阻力忽略不计,求: