题目内容
【题目】在用电火花计时器（或电磁打点计时器）研究匀变速直线运动的实验中，某同学打出了一条纸带，已知计时器打点的时间间隔为T=0.02s，他按打点先后顺序每5个点取1个计数点，得到了O、A、B、C、D等几个计数点，如图所示，则相邻两个计数点之间的时间间隔为s．用刻度尺量得A、B、C、D点到O点的距离分别为x1=1.50cm，x2=3.40cm，x3=5.70cm，x4=8.40cm．由此可知，打C点时纸带的速度表达式 ， 大小为m/s；与纸带相连小车的加速度表达式 ， 大小为m/s2 ． （以上数据取两位有效数字）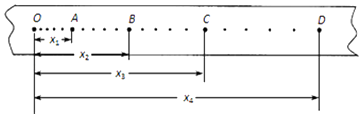
【答案】0.10；vC= 
；0.25；a= 
；0.40
【解析】解：由于每相邻两个计数点间还有4个点，所以相邻的计数点间的时间间隔T′=5T=0.10s，
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上C点时小车的瞬时速度大小．
vC= 
= 
= 
=0.25m/s
设0到A之间的距离为x1，以后各段分别为x2、x3、x4，
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，
得：x3﹣x1=2a1T2
x4﹣x2=2a2T2
为了更加准确的求解加速度，我们对两个加速度取平均值
得：a= 
（a1+a2）
即小车运动的加速度计算表达式为：a= 
= 
= 
m/s2=0.4m/s2
所以答案是：0.10，vC= ，0.25，a= ，0.40．
【考点精析】解答此题的关键在于理解匀变速直线运动的速度、位移、时间的关系的相关知识，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值，以及对匀变速运动中的平均速度的理解，了解平均速度：V=V0+Vt．
