题目内容
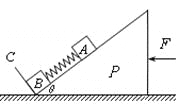
【题目】如图所示，在倾角为θ的光滑斜劈P的斜面上有两个用轻质弹簧相连的物块A、B，C为一垂直固定在斜面上的挡板。A、B质量均为m，斜面连同挡板的质量为M，弹簧的劲度系数为k，系统静止于光滑水平面。现开始用一水平恒力F作用于Ｐ，（重力加速度为g）下列说法中正确的是（ ）
A.若F=0，挡板受到B物块的压力为
B.力F较小时A相对于斜面静止，F大于某一数值，A相对于斜面向上滑动
C.若要B离开挡板C，弹簧伸长量需达到
D.若
且保持两物块与斜劈共同运动，弹簧将保持原长
【答案】AD
【解析】
A、F=0时，对物体A、B整体受力分析，受重力、斜面的支持力N1和挡板的支持力N2，根据共点力平衡条件，沿平行斜面方向，有N2-（2m）gsinθ=0，故压力为2mgsinθ，故A错误；
B、用水平力F作用于P时，A具有水平向左的加速度，设加速度大小为a，将加速度分解如图
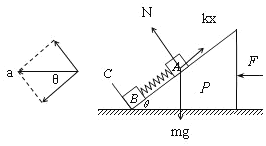
根据牛顿第二定律得
mgsinθ-kx=macosθ
当加速度a增大时，x减小，即弹簧的压缩量减小，物体A相对斜面开始向上滑行。故只要有力作用在P上，A即向上滑动，故B错误；
C、物体B恰好离开挡板C的临界情况是物体B对挡板无压力，此时，整体向左加速运动，对物体B受力分析，受重力、支持力、弹簧的拉力，如图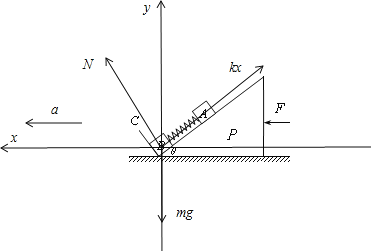
根据牛顿第二定律，有
mg-Ncosθ-kxsinθ=0
Nsinθ-kxcosθ=ma
解得：kx=mgsinθ-macosθ，
故C错误；
D、若F=（M+2m）gtanθ且保持两物块与斜劈共同运动，则根据牛顿第二定律，整体加速度为gtanθ；
对物体A受力分析，受重力，支持力和弹簧弹力，如图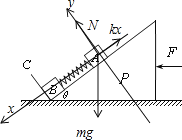
根据牛顿第二定律，有
mgsinθ-kx=macosθ
解得
kx=0
故弹簧处于原长，故D正确；
练习册系列答案
相关题目
