��Ŀ����
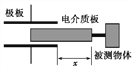
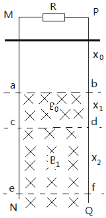
����Ŀ����ͼ��ʾ����ƽ���������⻬��������MN��PQ��ֱ���ã�������֮��ľ���ΪL=1m��������M��P֮��������R=0.2����������費�ƣ���abcd��������һ������ֱ��������ƽ������Ĵų��Ÿ�Ӧǿ��B0=1T���ų��Ŀ���x1=1m����cd��������������һ������Ҳ��ֱ�ڵ���ƽ������Ĵų��Ÿ�Ӧǿ��B1=0.5T��һ������Ϊm=1kg�Ľ�������ֱ���ڽ��������ϣ��뵼��Ӵ����ã��������ĵ���r=0.2����������������ab�����϶�x0�������ͷţ������������ų���ǡ��������ֱ���˶�������������ų������efʱϵͳ�ﵽ�ȶ�״̬��cd��ef֮��ľ���x2=15m����gȡ10m/s2��
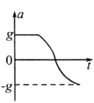
��1������������ų���ʱ���ٶȴ�С
��2���������ӿ�ʼ��ֹ���ų����дﵽ�ȶ�״̬���ʱ���е���R������������
��3����������ӿ�ʼ��ֹ���ڴų����дﵽ�ȶ�״̬��������ʱ�䣮
���𰸡���1��4m/s����2��QR=20 J��3��2.7875s
��������
��1������ڵ���ų��߽�abʱ���ٶ�Ϊv��������и�Ÿ��߲����ĸ�Ӧ�綯��Ϊ��![]()
��·�еĸ�Ӧ����Ϊ��I=![]()
�����������ֱ���˶�����ƽ�������ã�![]() ��
��
��ã�![]() =4m/s��
=4m/s��
��2������ڵ���ų��߽�efʱ���ٶ�Ϊv����������и�Ÿ��߲����ĸ�Ӧ�綯��Ϊ�� ![]()
��·�еĸ�Ӧ����Ϊ��I��=![]()
�����������ֱ���˶�����ƽ�������ã�![]() ��
��
��ã�![]() =16m/s��
=16m/s��
��������·�����Ľ�������Q���������غ㶨�ɿɵã�mgd=Q+![]() ��
��
���ڰ���R�ĵ���ֵ��ȣ����Բ����Ľ�������ȣ��ڰ�ͨ���ų����Ĺ�����R�����Ľ����� QR=![]() Q��
Q��
��ã�QR=20 J
��3���������ڴų��Ϸ��˶���ʱ�䣺![]()
���ڴų������˶���ʱ�䣺![]()
���ս���ų���ʱ���ٶ�Ϊ��v=4 m/s
����ڴų����˶��ٶ�Ϊvʱ���ٶ�Ϊa�������ڣ�mg��B1IL=ma
��![]() ��
��![]()
�ɵã�mg��![]() =m
=m![]()
���εã�mg��t��![]() ��t =m��v
��t =m��v
������͵ã� ��mg��t����![]() ��t =��m��v
��t =��m��v
�ã�mgt2��![]() =m��v�䩁v��
=m��v�䩁v��
�����ã�t2=2.1375 s
�������˶�����ʱ�䣺t=t0+t1+t2=0.4+0.25+2.1375=2.7875s