题目内容
在匀强磁场里有一个原来静止的放射性元素
U，由于发生α衰变而变为一种新元素钍核
Th，假设衰变时释放的核能全部转化为α粒子和钍核的动能，则α粒子和钍核的动能之比以及它们在磁场中运动的半径之比为（ ）
238 92 |
234 90 |
分析：根据动量守恒确定两粒子动量大小相等方向相反，然后根据公式R=
确定两粒子的半径之比根据Ek=
| mv |
| qB |
| p2 |
| 2m |
解答：解：动量P=mv，得v=
，Ek=
mv2=
衰变过程动量守恒，所以两种粒子合动量为0，动量大小相等方向相反，
所以EK：EK′=m′：m=234：4
根据动量守恒：mv=m′v′
R=
，动量相同所以
=
=
=
；
两粒子带同种电荷，运动方向相反，由左手定则知安培力方向相反，故为外接圆；
故选C．
| p |
| m |
| 1 |
| 2 |
| p2 |
| 2m |
衰变过程动量守恒，所以两种粒子合动量为0，动量大小相等方向相反，
所以EK：EK′=m′：m=234：4
根据动量守恒：mv=m′v′
R=
| mv |
| qB |
| R |
| R′ |
| q′ |
| q |
| 90 |
| 2 |
| 45 |
| 1 |
两粒子带同种电荷，运动方向相反，由左手定则知安培力方向相反，故为外接圆；
故选C．
点评：本题考查了动能与动量的关系式以及磁场中圆周运动的半径公式，知道衰变过程动量守恒是关键．
练习册系列答案
字词句段篇系列答案
相关题目
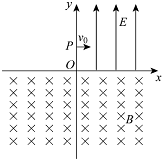（2004?南通模拟）如图所示，在xoy平面内，第I象限中有匀强电场，场强大小为E，方向沿y轴正方向，在x轴的下方有匀强磁场，磁感强度大小为B，方向垂直于纸面向里，今有一个质量为m，电荷量为e的电子（不计重力），从y轴上的P点以初速度v0垂直于电场方向进入电场．经电场偏转后，沿着与x轴正方向成45°进入磁场，并能返回到原出发点P．求：
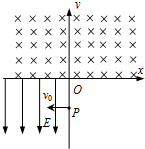如图所示，在xOy平面内的第Ⅲ象限中有沿-y方向的匀强电场，场强大小为E．在第I和第II象限有匀强磁场，方向垂直于坐标平面向里．有一个质量为m，电荷量为e的电子，从y轴的P点以初速度v0垂直于电场方向进入电场（不计电子所受重力），经电场偏转后，沿着与x轴负方向成45°角进入磁场，并能返回到原出发点P．
如图所示，在xoy面内，第一象限中有匀强电场，场强大小为E，方向 沿y轴正方向．在X轴的下方有匀强磁场，磁感应强度大小为B，方向垂直纸面向里．今有一个质量为m 电荷量为q的带负电的粒子（不计粒子的重力和其他 阻力），从y轴上的P点以初速度v0垂直于电场方向 进人电场．经电场偏转后，沿着与X正方向成30°进入 磁场．试完成：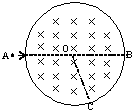
如图所示，圆形区域内有垂直于纸面向里的匀强磁场，一个带电粒子以速度v从A点沿 直径AOB方向射入磁场，经过时间t从C点射出磁场，OC与OB成60°角．现将带电粒子的速度变为
（2005?淮安二模）如图所示，在xoy平面内，第I象限中有匀强电场，场强大小为E，方向沿x轴负方向，在第Ⅱ象限和第Ⅲ象限有匀强磁场，方向垂直于纸面向里．今有一个质量为m，电荷量为e的质子（不计重力），从x轴上的P点以初速度v0垂直于电场方向进入电场．经电场偏转后，沿着与y轴正方向成45°角的方向进入磁场，从磁场中飞出时恰好能返回到原出发点P．试求：