题目内容
 (2005?淮安二模)如图所示,在xoy平面内,第I象限中有匀强电场,场强大小为E,方向沿x轴负方向,在第Ⅱ象限和第Ⅲ象限有匀强磁场,方向垂直于纸面向里.今有一个质量为m,电荷量为e的质子(不计重力),从x轴上的P点以初速度v0垂直于电场方向进入电场.经电场偏转后,沿着与y轴正方向成45°角的方向进入磁场,从磁场中飞出时恰好能返回到原出发点P.试求:
(2005?淮安二模)如图所示,在xoy平面内,第I象限中有匀强电场,场强大小为E,方向沿x轴负方向,在第Ⅱ象限和第Ⅲ象限有匀强磁场,方向垂直于纸面向里.今有一个质量为m,电荷量为e的质子(不计重力),从x轴上的P点以初速度v0垂直于电场方向进入电场.经电场偏转后,沿着与y轴正方向成45°角的方向进入磁场,从磁场中飞出时恰好能返回到原出发点P.试求:(1)P点离坐标原点的距离l;
(2)磁场的磁感应强度B;
(3)质子第二次在电场中运动的时间t.
分析:(1)分析质子的运动情况:质子从P到A,受到竖直向下的电场力而做类平抛运动(或匀变速曲线运动);进入磁场从A到C再到D,做匀速圆周运动;离开磁场从D到P,做匀速直线运动,画出轨迹.质子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动.在A点质子的速度与x轴成45°角,则知质子经过A点的速度为v=
v0.根据动能定理研究质子从P到A的过程,可求出h.
(2)由运动学公式,确定OA的距离,再由几何关系可确定,OD的距离,最后由圆弧半径的公式,即可求解;
(3)质子第二次在电场中做匀减速运动,由牛顿第二定律与运动学公式可求出时间.
| 2 |
(2)由运动学公式,确定OA的距离,再由几何关系可确定,OD的距离,最后由圆弧半径的公式,即可求解;
(3)质子第二次在电场中做匀减速运动,由牛顿第二定律与运动学公式可求出时间.
解答: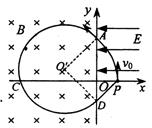 解:(1)质子运动的轨迹示意图如右图所示,质子进入电场从P到A,做类平抛运动(或匀变速曲线运动);进入磁场从A到C再到D,做匀速圆周运动;离开磁场从D到P,做匀速直线运动.
解:(1)质子运动的轨迹示意图如右图所示,质子进入电场从P到A,做类平抛运动(或匀变速曲线运动);进入磁场从A到C再到D,做匀速圆周运动;离开磁场从D到P,做匀速直线运动.
质子经过A点的速度大小:v=
=
v0
质子从P到A过程,由动能定理得:eEl=
mv2-
m
解得,l=
(2)设OA的距离为S1,OD的距离为S2,
则S1=v0t
l=
t
解得:S1=2l
质子从磁场中飞出时的方向与y轴也成45°,所以S2=l
所以,质子在磁场中的轨道半径为R=
=
由于R=
,解得:B=
(3)质子第二次在P点时,速度大小为
v0,速度方向与x轴正方向成45°,
质子第二次在电场中运动,在x方向做初速度为v0,
加速度大小为a=
的匀减速直线运动.
则有:-l=v0t-
t2
解得:t=(1+
)
答:
(1)P点离坐标原点的距离l=
;
(2)磁场的磁感应强度B=
;
(3)质子第二次在电场中运动的时间t=(1+
)
.
 解:(1)质子运动的轨迹示意图如右图所示,质子进入电场从P到A,做类平抛运动(或匀变速曲线运动);进入磁场从A到C再到D,做匀速圆周运动;离开磁场从D到P,做匀速直线运动.
解:(1)质子运动的轨迹示意图如右图所示,质子进入电场从P到A,做类平抛运动(或匀变速曲线运动);进入磁场从A到C再到D,做匀速圆周运动;离开磁场从D到P,做匀速直线运动. 质子经过A点的速度大小:v=
| v0 |
| cos45° |
| 2 |
质子从P到A过程,由动能定理得:eEl=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得,l=
m
| ||
| 2Ee |
(2)设OA的距离为S1,OD的距离为S2,
则S1=v0t
l=
| v0tan45° |
| 2 |
解得:S1=2l
质子从磁场中飞出时的方向与y轴也成45°,所以S2=l
所以,质子在磁场中的轨道半径为R=
| S1+S2 | ||
|
3
| ||
| 2 |
由于R=
| mvA |
| eB |
| 4E |
| 3v0 |
(3)质子第二次在P点时,速度大小为
| 2 |
质子第二次在电场中运动,在x方向做初速度为v0,
加速度大小为a=
| Ee |
| m |
则有:-l=v0t-
| 1 |
| 2 |
| Ee |
| m |
解得:t=(1+
| 2 |
| mv0 |
| Ee |
答:
(1)P点离坐标原点的距离l=
m
| ||
| 2Ee |
(2)磁场的磁感应强度B=
| 4E |
| 3v0 |
(3)质子第二次在电场中运动的时间t=(1+
| 2 |
| mv0 |
| Ee |
点评:质子在电场中做类平抛运动的研究方法是运动的分解,而磁场中圆周运动的研究方法是画轨迹,都常用的思路,难度不大.

练习册系列答案
相关题目



 (2005?淮安二模)如图所示,+Q为固定的正电荷,在它的电场中,一电荷量为+q的粒子,从a点以沿ab方向的初速度v0开始运动.若粒子只受电场力作用,则它的运动轨迹不可能是图中的( )
(2005?淮安二模)如图所示,+Q为固定的正电荷,在它的电场中,一电荷量为+q的粒子,从a点以沿ab方向的初速度v0开始运动.若粒子只受电场力作用,则它的运动轨迹不可能是图中的( ) (2005?淮安二模)有R1、R2、R3、R4四个电阻,其中三个电阻的阻值相等,只有一个电阻的阻值较大.为了找出阻值较大的这个电阻,某同学设计了如图所示的电路,当开关S闭合时,电流表G中有从b流向a的电流.则下列分析正确的是( )
(2005?淮安二模)有R1、R2、R3、R4四个电阻,其中三个电阻的阻值相等,只有一个电阻的阻值较大.为了找出阻值较大的这个电阻,某同学设计了如图所示的电路,当开关S闭合时,电流表G中有从b流向a的电流.则下列分析正确的是( )