题目内容
 如图所示,在xoy面内,第一象限中有匀强电场,场强大小为E,方向 沿y轴正方向.在X轴的下方有匀强磁场,磁感应强度大小为B,方向垂直纸面向里.今有一个质量为m 电荷量为q的带负电的粒子(不计粒子的重力和其他 阻力),从y轴上的P点以初速度v0垂直于电场方向 进人电场.经电场偏转后,沿着与X正方向成30°进入 磁场.试完成:
如图所示,在xoy面内,第一象限中有匀强电场,场强大小为E,方向 沿y轴正方向.在X轴的下方有匀强磁场,磁感应强度大小为B,方向垂直纸面向里.今有一个质量为m 电荷量为q的带负电的粒子(不计粒子的重力和其他 阻力),从y轴上的P点以初速度v0垂直于电场方向 进人电场.经电场偏转后,沿着与X正方向成30°进入 磁场.试完成:(1)求P点离坐标原点O的距离h;
(2)求粒子从P点出发到粒子第一次离开磁场时所用的时间?
(3)在其他条件不改变,只改变磁感应强度,当磁场的磁感应强度B取某一合适的数值,粒子离开磁场后能否返回到原出发点P?若能说明能的理由;若不能请说明不能的理由.
分析:(1)粒子经电场偏转后,沿着与X正方向成30°进入磁场,根据速度的方向结合平行四边形定则求出速度的大小,通过动能定理求出P点离坐标原点O的距离h.
(2)粒子在电场中做类平抛运动,在磁场中做匀速圆周运动,结合在电场中竖直方向上的分速度求出在电场中的运动时间,根据几何关系求出在磁场中运动的圆心角,结合周期公式求出粒子在磁场中的运动时间,从而得出粒子从P点出发到粒子第一次离开磁场时所用的时间.
(3)粒子进磁场和出磁场的速度方向与x轴的夹角相等,磁感应强度变化,轨道半径随着变化,出射点的位置随着变化,出磁场后做匀速直线运动,可以返回出发点P.
(2)粒子在电场中做类平抛运动,在磁场中做匀速圆周运动,结合在电场中竖直方向上的分速度求出在电场中的运动时间,根据几何关系求出在磁场中运动的圆心角,结合周期公式求出粒子在磁场中的运动时间,从而得出粒子从P点出发到粒子第一次离开磁场时所用的时间.
(3)粒子进磁场和出磁场的速度方向与x轴的夹角相等,磁感应强度变化,轨道半径随着变化,出射点的位置随着变化,出磁场后做匀速直线运动,可以返回出发点P.
解答:解:(1)由几何关系得:vy=
v0.
v=
v0
根据动能定理得:qEh=
mv2-
mv02
联立解得:h=
.
(2)在电场中运动的时间t1=
加速度a=
解得t1=
在磁场中运行的时间,由几何关系知:t2=
T
而周期T=
则t2=
所以共用时间t=t1+t2=
+
.
(3)能够返回到出发点P,只要B连续变化,则圆的半径就连续变化,由几何关系知,粒子在x轴上离开磁场的位置就可以连续变化,在第三象限没有电场和磁场,粒子在该象限做匀速直线运动,每次运动方向都与x轴正向成30度角,当B取某一合适数值时,粒子能够回到出发点.
答:(1)P点离坐标原点O的距离h=
.
(2)粒子从P点出发到粒子第一次离开磁场时所用的时间t=
+
.
(3)粒子能够回到出发点P.
| ||
| 3 |

v=
2
| ||
| 3 |
根据动能定理得:qEh=
| 1 |
| 2 |
| 1 |
| 2 |
联立解得:h=
| mv02 |
| 6qE |
(2)在电场中运动的时间t1=
| vy |
| a |
加速度a=
| qE |
| m |
解得t1=
| ||
| 3qE |
在磁场中运行的时间,由几何关系知:t2=
| 5 |
| 6 |
而周期T=
| 2πm |
| qB |
则t2=
| 5πm |
| 3qB |
所以共用时间t=t1+t2=
| ||
| 3qE |
| 5πm |
| 3qB |
(3)能够返回到出发点P,只要B连续变化,则圆的半径就连续变化,由几何关系知,粒子在x轴上离开磁场的位置就可以连续变化,在第三象限没有电场和磁场,粒子在该象限做匀速直线运动,每次运动方向都与x轴正向成30度角,当B取某一合适数值时,粒子能够回到出发点.
答:(1)P点离坐标原点O的距离h=
| mv02 |
| 6qE |
(2)粒子从P点出发到粒子第一次离开磁场时所用的时间t=
| ||
| 3qE |
| 5πm |
| 3qB |
(3)粒子能够回到出发点P.
点评:本题考查了带电粒子在电场中和磁场中的运动,知道粒子在电场中做类平抛运动,在磁场中做圆周运动,结合运动学公式灵活求解.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 =4×106C/kg的正离子,这些正离子的速率分别在0到2×106m/s的范围内,不计离子的重力及它们之间的相互作用。
=4×106C/kg的正离子,这些正离子的速率分别在0到2×106m/s的范围内,不计离子的重力及它们之间的相互作用。
 ×10-7s时这些离子所在位置构成的曲线方程。
×10-7s时这些离子所在位置构成的曲线方程。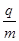 =4×106C/kg的正离子,这些正离子的速率分别在0到2×106m/s的范围内,不计离子的重力及它们之间的相互作用。
=4×106C/kg的正离子,这些正离子的速率分别在0到2×106m/s的范围内,不计离子的重力及它们之间的相互作用。
 ×10-7s时这些离子所在位置构成的曲线方程。
×10-7s时这些离子所在位置构成的曲线方程。