��Ŀ����
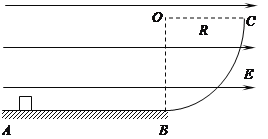
����Ŀ����ͼ1��ʾ��ľ��OA������O����ֱƽ����ת����ij�о�С�����ô�װ��̽�������ٶ�a��б����Ǧ�֮��Ĺ�ϵ����֪���ʼ���ܵ�������б�����ϡ���СΪF=8N�������ã��ɾ�ֹ��ʼ�˶�����������m=1kg��ͨ����θı�б����Ǧȣ��ظ�ʵ�飬�ò�õ������������ͼ2��ʾ��a���ȹ�ϵͼ�ߣ��������ľ���Ķ�Ħ������Ϊ0.2�������ľ�������Ħ�������ڻ���Ħ������gȡ10m/s2 �� ���ʣ�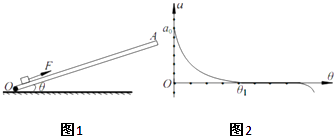
��1��ͼ����a�ύ��a0��
��2��ͼ������ύ�������1����Ĺ�ϵʽ��
��3�����ľ�峤L=2m�����Ϊ37�㣬�����F����������O�㿪ʼ�˶���Ϊ��֤��鲻���ľ�嶥�ˣ���F���õ��ʱ�䣮��ȡsin37��=0.6��cos37��=0.8��
���𰸡�
��1��
�⣺ͼ����a�ύ�㣬˵����=0��������ڦ�=0ʱ��ţ�ٵڶ����ɵã�F����mg=ma0��
��ã� ![]()
��2��
�⣺����=��1ʱ�У�F����mgcos�̩�mgsin��=0���������ݵã�
cos��+5sin��=4
��3��
�⣺��F�������ʱ��Ϊt��������F����ʱ���������������ţ�ٵڶ����ɵã�
F����mgcos�̩�mgsin��=ma1��
v=at1
x1= ![]() ��
��
��ȥF���������������ţ�ٵڶ����ɵã���mgcos��+mgsin��=ma2
v2=2a2��L��x1��
������ã�t=3.1s
����������1�������꽻���ʾľ��ˮƽ����ʱ�ļ��ٶȣ�����ţ�ٵڶ����ɼ�����⣻��2����ͼ������ύ�������1 �� ͨ������������ţ�ٵڶ����������ϵ��3������ţ�ٵڶ����ɷֱ������F�ͳ�ȥFʱ�ļ��ٶȣ������ȱ���ֱ���˶��Ļ�����ʽ������������̵�λ�ƣ���������λ��֮��ΪL��⣮