题目内容
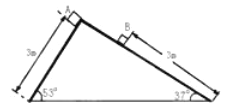
【题目】如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软丝绸。丝绸恰好将两侧斜面覆盖,现将质量为![]() 的A物体和质量为
的A物体和质量为![]() 的B物体轻放在丝绸上,如图示的位置开始计时,斜面长度及斜面倾角图中已标出,已知
的B物体轻放在丝绸上,如图示的位置开始计时,斜面长度及斜面倾角图中已标出,已知![]() =3kg,
=3kg, ![]() =1kg,A与丝绸间的动摩擦因数
=1kg,A与丝绸间的动摩擦因数![]() =
=![]() ,B与丝绸间的动摩擦因数
,B与丝绸间的动摩擦因数![]() =
=![]() ,假设两物体与丝绸间的滑动摩擦力与最大静摩擦力相等,初始时A距高斜面底端3m,B距离斜面底端也为3m。两物体可视为质点。试求从计时开始,A、B两物体到达斜面底端所用时间分别为多少。(sin37°=0.6,cos37°=0.8,g取10m/s)
,假设两物体与丝绸间的滑动摩擦力与最大静摩擦力相等,初始时A距高斜面底端3m,B距离斜面底端也为3m。两物体可视为质点。试求从计时开始,A、B两物体到达斜面底端所用时间分别为多少。(sin37°=0.6,cos37°=0.8,g取10m/s)
【答案】1s 2s
【解析】试题分析:先假设纸带不动,判断出物体A和B的受力情况;然后得到物体A和B的实际运动情况,然后结合牛顿第二定律和运动学公式列式求解。
先假设绸带固定不动,再把物体A、B按题中条件放置在斜面上
对A物体受力分析可得: ![]() ,则A相对绸带滑动;
,则A相对绸带滑动;
对B物体受力分析可得: ![]() ,则B相对绸带不滑动;
,则B相对绸带不滑动;
对B和绸带整体分析,A对绸带滑动摩擦力![]() N,
N,
B物体沿斜面分力![]() N
N
则说明若A、B和绸带同时释放后,B和绸带先静止不动,A沿绸带加速下滑3m后,B再拖动绸带一起沿光滑斜面加速下滑.
A沿绸带下滑过程中,根据牛顿第二定律:![]() -
-![]()
代入数据解得: ![]() 6m/s
6m/s
根据位移时间公式,有![]()
代入数据解得: ![]()
B拖动绸带一起沿光滑斜面加速下滑过程中:
根据牛顿第二定律: ![]()
代入数据解得: ![]() 6m/s
6m/s
根据位移时间公式,有![]()
解得: ![]()
则从开始计时的时间![]()

练习册系列答案
相关题目