题目内容
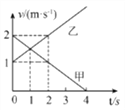
【题目】如图1所示,一个圆形线圈的匝数n=1000匝,线圈面积S=0.02m2 , 线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间的变化规律如图2所示.求
(1)在0~4s内穿过线圈的磁通量变化量;
(2)前4s内产生的感应电动势;
(3)6s内通过电阻R的电荷量q.
【答案】
(1)解:根据磁通量定义式=BS,那么在0~4s内穿过线圈的磁通量变化量为:
△=(B2﹣B1)S=(0.4﹣0.2)×0.02Wb=4×10﹣3Wb;
答:在0~4s内穿过线圈的磁通量变化量4×10﹣3Wb;
(2)解:由图象可知前4 s内磁感应强度B的变化率为:
![]() =
= ![]() T/s=0.05 T/s
T/s=0.05 T/s
4 s内的平均感应电动势为:
E=nS ![]() =1000×0.02×0.05 V=1 V.
=1000×0.02×0.05 V=1 V.
答:前4s内感应电动势为1V.
(3)解:电路中的平均感应电流为: ![]() =
= ![]() ,
,
q= ![]() t,
t,
又因为E=n ![]() ,
,
所以q=n ![]() =1000×
=1000× ![]() C=0.8 C.
C=0.8 C.
答:6s内通过R的电荷量为0.8C.
【解析】(1)依据图象,结合磁通量定义式=BS,即可求解;(2)根据法拉第电磁感应定律,结合磁感应强度的变化率求出前4s内感应电动势的大小.(3)根据感应电动势,结合闭合电路欧姆定律、电流的定义式求出通过R的电荷量.
【考点精析】掌握电磁感应与电路是解答本题的根本,需要知道用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向;画等效电路;运用全电路欧姆定律,串并联电路性质,电功率等公式联立求解.

练习册系列答案
相关题目