题目内容
12. 如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,B、C分别为半圆轨道的最低点和最高点.一个质量m=0.1kg的小物体P被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上.此时P到B点的距离x0=0.5m,在墙壁和P之间夹一根被压缩的轻弹簧(弹簧的压缩量小于x0).物体P与水平轨道间的动摩擦因数μ=0.2,半圆轨道半径R=0.4m.现将细线剪断,P被弹簧向右弹出后滑上半圆轨道,并恰好能经过C点.g取10m/s2.求:
如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,B、C分别为半圆轨道的最低点和最高点.一个质量m=0.1kg的小物体P被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上.此时P到B点的距离x0=0.5m,在墙壁和P之间夹一根被压缩的轻弹簧(弹簧的压缩量小于x0).物体P与水平轨道间的动摩擦因数μ=0.2,半圆轨道半径R=0.4m.现将细线剪断,P被弹簧向右弹出后滑上半圆轨道,并恰好能经过C点.g取10m/s2.求:(1)小物体P到达C点的速度大小;
(2)小物体P经过B点时对轨道的压力;
(3)细线未剪断时弹簧的弹性势能.
分析 (1)根据P恰好能经过C点得出C速度,根据P从B到C的过程中机械能守恒求解经过B点时的速度;
(2)再运用牛顿第二定律求解经过B点时对轨道的压力.
(3)从剪断细线到P经过B点的过程中,由能量守恒求解.
解答 解:(1)P恰好能经过C点,设其速度为vc,
由向心力公式有$mg=m\frac{v_c^2}{R}$
解得${v_c}=\sqrt{gR}=\sqrt{10×0.4}=2m/s$
(2)P从B到C的过程中机械能守恒,设P经过B点时的速度为vB,则有$mg×2R+\frac{1}{2}mv_C^2=\frac{1}{2}mv_B^2$
解得${v_B}=\sqrt{4gR+v_C^2}=\sqrt{4×10×0.4+{2^2}}=2\sqrt{5}m/s$
设小球刚过B时受到圆轨道的支持力为NB,由向心力公式有${N_B}-mg=m\frac{v_B^2}{R}$
解得 ${N_B}=mg+m\frac{v_B^2}{R}=0.1×10+0.1×\frac{{{{(2\sqrt{5})}^2}}}{0.4}=6N$
由牛顿第三定律可得,
物体刚过B点时对轨道的压力大小为6N,方向竖直向下.
(3)设细线剪断前弹簧的弹性势能为EP.从剪断细线到P经过B点的过程中,由能量守恒可得${E_P}-μmg{x_0}=\frac{1}{2}mv_B^2$
解得${E_P}=μmg{x_0}+\frac{1}{2}mv_B^2=0.2×0.1×10×0.5+\frac{1}{2}×0.1×{(2\sqrt{5})^2}=1.1J$
答:(1)小物体P到达C点的速度大小是2m/s;
(2)小物体P经过B点时对轨道的压力是6N,方向向下;
(3)细线未剪断时弹簧的弹性势能是1.1J.
点评 本题是能量守恒与牛顿运动定律的综合应用,来处理圆周运动问题.基础题.利用功能关系解题的优点在于不用分析复杂的运动过程,只关心初末状态即可,平时要加强训练深刻体会这一点.

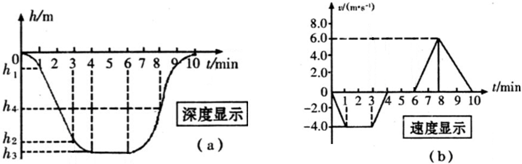
| A. | (a)图中h3代表本次最大深度,应为720m | |
| B. | 全过程中最大加速度是0.05m/s2 | |
| C. | 潜艇内人员感到超重发生在0-1min和8-10min的时间段内 | |
| D. | 潜艇在8-10min时间段内机械能守恒 |
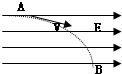 方向水平向右的匀强电场中,一带电粒子从A点飞入,B点飞出,粒子运动轨迹如图,则有关带电粒子的判断错误的是(重力不计)( )
方向水平向右的匀强电场中,一带电粒子从A点飞入,B点飞出,粒子运动轨迹如图,则有关带电粒子的判断错误的是(重力不计)( )| A. | 一定带负电 | B. | 可能带正电,也可能带负电 | ||
| C. | 在电场中作减速运动,电势能增加 | D. | 受到的电场力一定水平向左 |
| A. | 速度变化大,加速度就大,且加速度数值不断变小,速度也不断变小 | |
| B. | 能选择作为参考系的物体一定是静止不动的 | |
| C. | 合力是由分力叠加而成,所以合力一定大于分力 | |
| D. | 惯性是物体的固有属性,只跟物体的质量有关,跟其他因素无关 |
| A. | 在两板间插入玻璃板 | |
| B. | 使两板靠近些 | |
| C. | 保持两板的间距不变,使两板错开些 | |
| D. | 以上做法都不对 |
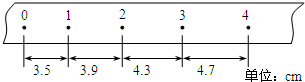
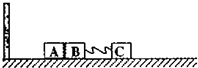 如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在BC之间的弹簧第一次恢复到原长时追上B,并且在碰撞后和B粘到一起.求:
如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在BC之间的弹簧第一次恢复到原长时追上B,并且在碰撞后和B粘到一起.求: 如图所示,在xoy平面内,直线MN与x轴正方向成30°角,MN下方是垂直于纸面向外的匀强磁场,MN与y轴正方向间存在电场强度E=$\frac{2}{3}×1{0^6}N/C$的匀强电场,其方向与y轴正方向成60°角且指向左上方,一带正电的粒子(重力不计),从坐标原点O沿x轴正方向进入磁场,测得该粒子经过磁场的时间t1=$\frac{π}{6}×{10^{-6}}s$,已知粒子的比荷$\frac{q}{m}$=107C/kg.试求:
如图所示,在xoy平面内,直线MN与x轴正方向成30°角,MN下方是垂直于纸面向外的匀强磁场,MN与y轴正方向间存在电场强度E=$\frac{2}{3}×1{0^6}N/C$的匀强电场,其方向与y轴正方向成60°角且指向左上方,一带正电的粒子(重力不计),从坐标原点O沿x轴正方向进入磁场,测得该粒子经过磁场的时间t1=$\frac{π}{6}×{10^{-6}}s$,已知粒子的比荷$\frac{q}{m}$=107C/kg.试求: