题目内容
17.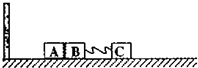 如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在BC之间的弹簧第一次恢复到原长时追上B,并且在碰撞后和B粘到一起.求:
如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在BC之间的弹簧第一次恢复到原长时追上B,并且在碰撞后和B粘到一起.求:(1)炸药爆炸后瞬间A、B的速度大小;
(2)在A追上B之前弹簧弹性势能的最大值;
(3)BC之间的弹簧第一次恢复到原长时B的速度;
(4)A与B相碰以后弹簧弹性势能的最大值.
分析 (1)炸药爆炸时,A、B分离,该过程中A、B动量守恒,爆炸产生的能量转化为A、B的动能,依据动量守恒和功能关系可正确解答.
(2)爆炸后,以B、C弹簧组成的系统为研究对象,系统水平方向动量守恒,当弹簧压缩最短时弹性势能最大,A、B速度相等,系统损失动能最大,损失的动能全部转化为弹性势能.
(3)A反弹后,当A与B碰撞瞬动量守恒,碰后成为一个整体,损失能量最大,然后以A、B、C三者以及弹簧组成的系统为研究对象,系统动量守恒,由此求出B 速度;
(4)当三者速度相等时,损失动能最大,全部转化为弹性势能.
解答 解:(1)塑胶炸药爆炸瞬间取A和B为研究对象,假设爆炸后瞬间A、B的速度大小分别为vA、vB,取向右为正方向,由动量守恒定律:
mBvB-mAvA=0
爆炸产生的热量有9J转化为A、B的动能,有:$E=\frac{1}{2}{m}_{A}{v}_{A}^{2}\;\;+\frac{1}{2}{m}_{B}{v}_{B}^{2}$
代入数据解得:vA=vB=3.0 m/s
故塑胶炸药爆炸后瞬间A与B的速度为:vA=vB=3.0 m/s.
(2)由于A在炸药爆炸后再次追上B的时候弹簧恰好第一次恢复到原长,则在A追上B之前弹簧已经有一次被压缩到最短(即弹性势能最大).爆炸后取B、C和弹簧为研究系统,当弹簧第一次被压缩到最短时B、C达到共速vBC,此时弹簧的弹性势能最大,设为Ep1.
由动量守恒定律,得:mBvB=(mB+mC)vBC
由机械能守恒,得:$\frac{1}{2}{m}_{B}{v}_{B}^{2}=\frac{1}{2}({m}_{B}+{m}_{C})\;\;{v}_{BC}^{2}+{E}_{P1}$
代入数据得:EP1=3.0 J.
故在A追上B之前弹簧弹性势能的最大值为EP1=3.0 J.
(3)设B、C之间的弹簧第一次恢复到原长时B、C的速度大小分别为vB1和vC1,则由动量守恒定律和能量守恒定律:
mBvB=mBvB1+mCvC1
$\frac{1}{2}{m}_{B}{v}_{B}^{2}=\frac{1}{2}{m}_{B}{v}_{B1}^{2}+\frac{1}{2}{m}_{C\;}{v}_{c1}^{2}$
代入数据解得:vB1=-1.0m/s,vC1=2.0m/s
(4)A爆炸后先向左匀速运动,与弹性挡板碰撞以后速度大小不变,反向弹回.当A追上B,发生碰撞瞬间达到共速vAB,由动量守恒定律
mAvA+mBvB1=(mA+mB)vAB
解得:vAB=1.0m/s
当A、B、C三者达到共同速度vABC时,弹簧的弹性势能最大为EP2,由动量守恒定律
(mA+mB)vAB+mCvC1=(mA+mB+mC)vABC
由机械能守恒定律,得:
$\frac{1}{2}({m}_{A}+{m}_{B})\;\;{v}_{AB}^{2}+\frac{1}{2}{m}_{C}{v}_{C1}^{2}=\frac{1}{2}({m}_{A}+{m}_{B}+{m}_{C})\;{v}_{ADC}^{2}+{E}_{P2}$
代入数据解得:EP2=0.5J.
故A与B相碰以后弹簧弹性势能的最大值为:EP2=0.5J.
答:(1)炸药爆炸后瞬间A、B的速度大小都是3m/s;
(2)在A追上B之前弹簧弹性势能的最大值是3.0J;
(3)BC之间的弹簧第一次恢复到原长时B的速度是-1.0m/s;
(4)A与B相碰以后弹簧弹性势能的最大值是0.5J.
点评 本题考查了与弹簧有关的动量、能量问题,有一定综合性,易错点在于A反弹后与B碰撞过程中有能量损失,很多学生容易忽略这点,导致错误.


| A. | 2s后,甲、乙两物体的速度方向相反 | |
| B. | 甲做匀速直线运动,乙做变速直线运动 | |
| C. | 两物体两次速度相等的时刻分别是在1s末和4s末 | |
| D. | 乙在前2s内做匀加速直线运动,2s后做匀减速直线运动 |
 物理课上,老师做了一个奇妙的“跳环实验”.如图,她把一个带铁芯的线圈L、开关S和电源用导线连接起来后,将一铝质套环置于线圈L上,且使铁芯穿过套环.闭合开关S的瞬间,套环立刻跳起.
物理课上,老师做了一个奇妙的“跳环实验”.如图,她把一个带铁芯的线圈L、开关S和电源用导线连接起来后,将一铝质套环置于线圈L上,且使铁芯穿过套环.闭合开关S的瞬间,套环立刻跳起.某同学另找来器材再探究此实验.他连接好电路,并将线圈上端与电源正极相连,经重复试验,置于线圈上的套环未动.对比老师演示的实验,下列四个选项中,导致套环未动的原因可能是( )
| A. | 线圈接在了直流电源上 | B. | 线圈与电源的正、负极接反了 | ||
| C. | 所选线圈的匝数过多 | D. | 所用套环的材料与老师的不同 |
 如图,a、b、c、d是匀强电场中的四个点,它们正好是一个梯形的四个顶点.电场线与梯形所在的平面平行.ab平行cd,且cd边长为ab边长的三倍,已知a点的电势是2V,b点的电势是6V,c点的电势是20V.由此可知,d点的电势为( )
如图,a、b、c、d是匀强电场中的四个点,它们正好是一个梯形的四个顶点.电场线与梯形所在的平面平行.ab平行cd,且cd边长为ab边长的三倍,已知a点的电势是2V,b点的电势是6V,c点的电势是20V.由此可知,d点的电势为( )| A. | 2 V | B. | 6 V | C. | 8 V | D. | 12 V |
 在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如表:
在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m数据如表:| 次 数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 小车加速度a/m•s-2 | 1.98 | 1.72 | 1.48 | 1.25 | 1.00 | 0.75 | 0.48 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 0.75 | 1.00 | 1.67 |
| 小车质量的倒数1/m/kg-1 | 4 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.33 | 1.00 | 0.60 |
 如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,B、C分别为半圆轨道的最低点和最高点.一个质量m=0.1kg的小物体P被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上.此时P到B点的距离x0=0.5m,在墙壁和P之间夹一根被压缩的轻弹簧(弹簧的压缩量小于x0).物体P与水平轨道间的动摩擦因数μ=0.2,半圆轨道半径R=0.4m.现将细线剪断,P被弹簧向右弹出后滑上半圆轨道,并恰好能经过C点.g取10m/s2.求:
如图所示,粗糙水平轨道AB与竖直平面内的光滑半圆轨道BC在B处平滑连接,B、C分别为半圆轨道的最低点和最高点.一个质量m=0.1kg的小物体P被一根细线拴住放在水平轨道上,细线的左端固定在竖直墙壁上.此时P到B点的距离x0=0.5m,在墙壁和P之间夹一根被压缩的轻弹簧(弹簧的压缩量小于x0).物体P与水平轨道间的动摩擦因数μ=0.2,半圆轨道半径R=0.4m.现将细线剪断,P被弹簧向右弹出后滑上半圆轨道,并恰好能经过C点.g取10m/s2.求: