题目内容
14．
一质点沿着半径r=1m的圆周以n=2r/s的转速匀速运动，如图所示：试求：（1）从A点开始计时，经过$\frac{1}{4}$s的时间质点速度的变化；
（2）质点的向心加速度的大小．
分析 根据转速求出角速度，从而求出周期和线速度，进而求出经过$\frac{1}{4}$s的时间质点速度的变化；
根据向心加速度公式求出加速度．
解答 解：圆周运动的角速度ω=2πn=4πrad/s，周期T=$\frac{2π}{ω}=\frac{1}{2}s$，线速度v=ωr=4πm/s，
$t=\frac{1}{4}s=\frac{1}{2}T$，
以A点速度方向为正，则经过$\frac{1}{4}$s的时间质点速度的变化△v=-4π-4π=-8πm/s，
质点的向心加速度的大小为：a=（2πn）2r=16π2m/s2．
答：（1）从A点开始计时，经过$\frac{1}{4}$s的时间质点速度的变化为-8πm/s；
（2）质点的向心加速度的大小为16π2m/s2．
点评 本题主要考查了向心加速度公式的直接应用，难度不大，属于基础题．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
8．以下关于电场和电场线说法中正确的是（ ）
| A． | 电场、电场线都是客观存在的物质 | |
| B． | 在电场中，凡是电场线通过的点场强不为零，不画电场线区域内的点的场强为零 | |
| C． | 同一检验电荷在电场线疏密不同的地方所受的电场力一样大 | |
| D． | 电场线是人们假设的用以形象地表示电场强弱和方向的曲线，客观上是并不存在的 |
如图甲所示，比荷$\frac{q}{m}$=k均带正电荷的粒子（可视为质点），以速度v0从A点沿AB方向射入长方形磁场区域，长方形的长AB=$\sqrt{3}L$，宽AD=L，取粒子刚进入长方形区域的时刻为0时刻．垂直于长方形平面的磁感应强度如图乙所示变化（以垂直纸面向外的磁场方向为正方向），粒子仅在洛伦磁力的作用下运动．
如图所示，在倾角为θ的斜面上，沿斜面方向铺两条足够长的平行光滑导轨，两导轨间距为L，两者的底端用阻值为R的电阻相连，在导轨上垂直于导轨放有一根质量为m的金属杆cd，整个装置处于垂直于斜面的匀强磁场中，当金属杆cd匀速下滑时，R中电流的方向为从a到b，R消耗的电功率为P，导轨和金属杆cd的电阻都忽略不计，重力加速度为g，求：
如图所示，BC是半径为R的$\frac{1}{4}$圆弧形的光滑且绝缘的轨道，位于竖直平面内，其下端与水平绝缘轨道平滑连接，整个轨道处在水平向左的匀强电场中，电场强度为E，P为一质量为m，带正电q的小滑块（体积很小可视为质点），重力加速度为g．
如图所示，长L=9m、质量M=30kg的木板静止放在光滑水平面上，质量m=10kg的小物体放在木板的右端，木板和物块间的动摩擦因数μ=0.2．现对木板施加一水平向右的恒定拉力F，小物块可视为质点，物块受到的最大静摩擦力等于滑动摩擦力，g取10m/s2，求：
如图所示，在半径为R的半圆区域内存在着垂直纸面的匀强磁场（图中未画），磁感应强度为B，AD为半圆的直径，O为圆心．质量为m带电量为q的某种粒子由静止经电场加速后从O点垂直AD及磁场射入磁场中．（粒子重力不计）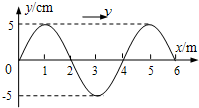
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图，波的传播速度v=2m/s，试求：