题目内容
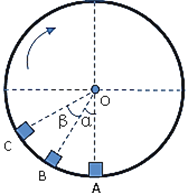
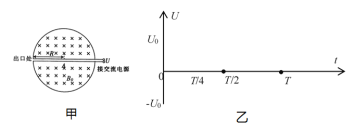
【题目】回旋加速器的工作原理如图甲所示,置于高真空中的D形金属盒半径为R,两盒间距很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B0的匀强磁场与盒面垂直。在下极板的圆心A处粒子源产生的粒子,质量为m电荷量为+q,在加速器中被加速,加速电压u随时间的变化关系如图乙所示![]() 。加速过程中不考虑相对论效应和变化电场对磁场分布的影响。
。加速过程中不考虑相对论效应和变化电场对磁场分布的影响。
(1)粒子开始从静止被加速,估算该离子离开加速器时获得的动能Ek;
(2)调节交流电的电压,先后两次的电压比为1:2,则粒子在加速器中的运动时间之比为多少?
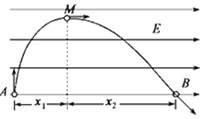
(3)带电粒子在磁场中做圆周运动的圆心并不是金属盒的圆心O,而且在不断的变动。设第一次加速后做圆周运动的圆心O1到O的距离为x1,第二次加速后做圆周运动的圆心O2到O的距离为x2,这二个距离平均值约为最后从加速器射出时圆周运动的圆心位置x,求x的值,并说明出口处为什么在A的左边;
(4)实际使用中,磁感应强度B会出现波动,若在t=![]() 时粒子第一次被加速,要实现连续n次加速,求B可波动的最大范围。
时粒子第一次被加速,要实现连续n次加速,求B可波动的最大范围。
【答案】(1)![]() ;(2)2:1;(3)
;(2)2:1;(3)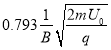 ;第一次圆周运动的圆心在A点的左边,最后一次圆周运动与左边相切,所以出口在A点的左边;(4)
;第一次圆周运动的圆心在A点的左边,最后一次圆周运动与左边相切,所以出口在A点的左边;(4)![]() ,n=2、3……
,n=2、3……
【解析】
根据回旋加速器原理,粒子在电场中加速,在磁场中偏转,根据轨道半径与运动周期可求运动动能及运动时间,若磁场出现波动,求出磁感强度的最大值和最小值,从而确定磁感强度的范围。
(1)圆周运动的最大半径约为R
![]()
离子离开加速器时获得的动能
![]()
(2)设加速n次
![]()
![]()
![]()
运动时间之比
![]()
(3)设第一、二次圆周运动的半径为r1和r2
![]()
![]()
![]()
![]()
![]()
![]()
可得
![]()
第一次圆周运动的圆心在A点的左边,最后一次圆周运动与左边相切,所以出口在A点的左边。
(4)设磁感应强度偏小时为B1,圆周运动的周期为T1
![]()
![]()
解得
![]()
设磁感应强度偏大时为B2,圆周运动的周期为T2
![]()
![]()
解得
![]()
因此
![]() ,n=2、3……
,n=2、3……

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案