题目内容
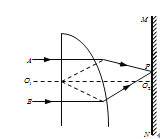
【题目】弧形轨道的下端与竖直圆轨道相接，质量为1kg的小球从高h=20 m的弧形轨道上端由静止滚下，小球进入圆轨道下端后沿圆轨道运动，圆轨道的半径为R=5m，(ｇ取10 m/s2)
试求：
（1）小球进入圆轨道最低点时的速度的大小；
（2）小球进入圆轨道最低点时对轨道的压力的大小
【答案】(1)20m/s (2)90N
【解析】试题分析（1）根据机械能守恒求得小球在M点的速度，（2）根据牛顿第二定律可求得轨道对小球的支持力，根据牛顿第三定律可以求出小球在最低点对轨道的压力大小。
（1）小球滑至最低点，由机械能守恒定律得：
解得：
（2）对小球在最低点受力分析，根据牛顿第二定律得：
解得：
根据牛顿第三定律可知小球在最低点对轨道的压力大小为90N.
练习册系列答案
相关题目
