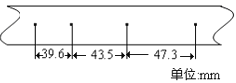
��Ŀ����
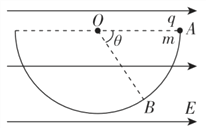
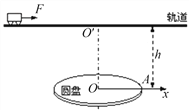
����Ŀ����ͼ��ʾ���뾶R=0.4 m��Բ��ˮƽ���ã�����ֱ��![]() ����ת������Բ��O���Ϸ�h=0.8 m�ߴ��̶�һˮƽ�������ת�ύ��
����ת������Բ��O���Ϸ�h=0.8 m�ߴ��̶�һˮƽ�������ת�ύ��![]() �㡣һ����m=1 kg��С��������Ϊ�ʵ㣩���ع���˶����ֶ���ʩ��һˮƽ����F=4 N��ʹ���
�㡣һ����m=1 kg��С��������Ϊ�ʵ㣩���ع���˶����ֶ���ʩ��һˮƽ����F=4 N��ʹ���![]() ���2 m���ɾ�ֹ��ʼ�ع�������˶�����С���˶���
���2 m���ɾ�ֹ��ʼ�ع�������˶�����С���˶���![]() ��ʱ����С���������ͷ�һС��ʱԲ�̵İ뾶OA��������ƽ�У���A����O���ҲࡣС��������Ķ�Ħ��������=0.2��gȡ10 m/s2��
��ʱ����С���������ͷ�һС��ʱԲ�̵İ뾶OA��������ƽ�У���A����O���ҲࡣС��������Ķ�Ħ��������=0.2��gȡ10 m/s2��
(1)��С��պ��䵽A�㣬��С���˶���![]() ����ٶȴ�С��
����ٶȴ�С��
(2)ΪʹС��պ�����A�㣬Բ��ת���Ľ��ٶ�ӦΪ���
(3)ΪʹС�����䵽Բ���ϣ�С����ˮƽ����F����ʱ�˶��ľ��뷶ΧӦΪ���
���𰸡���1��![]() ��2��
��2��![]() ��3��1~1.125 m
��3��1~1.125 m
��������
���⣨1������뿪O�������ƽ���˶����������ƽ���˶���ʱ���ƽ���˶��ij��ٶȣ��Ӷ��ó�С���˶���O�����ٶȣ�2����Բ��תһȦ�����ǡ�õ���СͰ����ʱ������ʱ����̣�Բ��תһȦ��ʱ����ƽ���˶�ʱ������ȣ��Ӷ��ó�Բ��ת���Ľ��ٶ���Сֵ��Ҳ�п�����ƽ���˶�ʱ���ڣ�Բ��ת��NȦ��������ת�����ٶȣ�
��3��С��������Բ���ϣ��������ƽ���˶��������С���׳����ٶȷ�Χ���Ӷ��ó�С��ļ��ٶȵķ�Χ����������ţ�ٵڶ����ɿ����ˮƽ�����ľ��뷶Χ��
�⣺��1��С���뿪С�������ڹ��ԣ������뿪С��ʱ���ٶ���ƽ���˶���![]()
R=vt
С���˶���O������ٶ�v=![]() =1m/s
=1m/s
��2��ΪʹС��պ�����A�㣬��С�������ʱ��ΪԲ��ת�����ڵ�����������![]() ������k=1��2��3��
������k=1��2��3��
��![]() rad/s������k=1��2��3��
rad/s������k=1��2��3��
��3��С�������䵽Բ���ϣ�����O������ٶȷ�Χ�ǣ�0��v��1m/s
��ˮƽ�������õ���С������������ֱ�Ϊx1��x2����Ӧ����O������ٶȷֱ�Ϊ0��1m/s��
�ɶ��ܶ������� Fx1����mgx0=0
�������ݽ��x1=1m
���ݶ��ܶ�������![]()
�������ݽ��x2=1.125m��![]() m
m
��ˮƽ����F���õľ��뷶Χ 1m��x��1.125m
�𣺣�1����С��պ��䵽A�㣬��С���˶���O������ٶ�1m/s��
��2��ΪʹС��պ�����A�㣬Բ��ת���Ľ��ٶ�ӦΪ![]() rad/s������k=0��1��2��3��
rad/s������k=0��1��2��3��
��3��ΪʹС�����䵽Բ���ϣ���ˮƽ����F���õľ��뷶Χ 1m��x��1.125m

 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�