题目内容
1.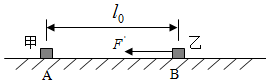 如图所示,足够大的光滑水平面上的A点固定有质量为M的甲滑块,B点放有质量为m的乙滑块,A、B两点间的距离为l0.甲、乙两滑块间存在相互作用的斥力F:方向在两滑块的连线上,大小与两滑块的质量的乘积成正比、与它们之间距离的二次方成反比,比例系数为k.先将B点的乙滑块由静止释放,释放时的乙滑块即刻又受到一个大小为F′=k$\frac{Mm}{4{{l}_{0}}^{2}}$、方向沿两滑块的连线并指向甲滑块的水平恒力作用,两滑块均可视为质点.
如图所示,足够大的光滑水平面上的A点固定有质量为M的甲滑块,B点放有质量为m的乙滑块,A、B两点间的距离为l0.甲、乙两滑块间存在相互作用的斥力F:方向在两滑块的连线上,大小与两滑块的质量的乘积成正比、与它们之间距离的二次方成反比,比例系数为k.先将B点的乙滑块由静止释放,释放时的乙滑块即刻又受到一个大小为F′=k$\frac{Mm}{4{{l}_{0}}^{2}}$、方向沿两滑块的连线并指向甲滑块的水平恒力作用,两滑块均可视为质点.(1)求乙滑块在释放时的加速度;
(2)求当乙滑块速度达到最大的vm的过程中,斥力所做的功;
(3)请定性地描述乙滑块在释放后的运动情况(只要求说明速度的大小变化及运动方向的情况)
分析 (1)根据牛顿第二定律求出乙滑块在释放时的加速度.
(2)当乙滑块水平方向上受到两个力大小相等时,乙球的速度最大,根据平衡求出移动的距离,根据动能定理求出斥力所做的功.
(3)通过合力方向与加速度方向相同,当加速度方向与速度方向相同时,做加速运动,当加速度方向与速度方向时,做减速运动,进行分析.
解答 解:(1)由牛顿第二定律有:F合=ma,
由题意可知,合力F合=k$\frac{Mm}{{l}_{0}^{2}}$-k$\frac{Mm}{4{l}_{0}^{2}}$
解得a=$\frac{3kM}{4{l}_{0}^{2}}$,方向水平向右.
(2)当乙滑块水平方向上受到两个力大小相等时,乙球的速度最大,为vm.
所以有:k$\frac{Mm}{4{l}_{0}^{2}}$=k$\frac{Mm}{{x}^{2}}$,
得x=2l0.
即:当乙向右滑过l0时速度达到最大,此过程中由动能定理可得:
$\frac{1}{2}$mvm2-0=WF-WF'
且WF′=$\frac{kMm}{4{l}_{0}^{2}}$•l0=$\frac{kMm}{4{l}_{0}}$
故斥力所做的功为:WF=$\frac{1}{2}$mvm2+$\frac{kMm}{4{l}_{0}}$;
(3)乙滑块先做远离甲的运动,速度先增大后减小,然后又反向做速度先增大后减小的运动,返回到释放点B后,再重复前面的运动,之后在B点和最远端之间做往复运动.
答:(1)乙滑块在释放时的加速度$\frac{3kM}{4{l}_{0}^{2}}$,方向水平向右.
(2)斥力所做的功$\frac{1}{2}$mvm2+$\frac{kMm}{4{l}_{0}}$.
(3)乙滑块先做远离甲的运动,速度先增大后减小,然后又反向做速度先增大后减小的运动,返回到释放点B后,再重复前面的运动,之后在B点和最远端之间做往复运动.
点评 本题综合考查了动能定理和牛顿第二定律,注意明确物理过程,重点是知道乙滑块水平方向上受到两个力大小相等时,乙球的速度最大.

| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 | |
| C. | 在定义加速度时,a=$\frac{△v}{△t}$,采用了比值定义法 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
| A. | 1:1 | B. | 2:1 | C. | 3:2 | D. | 4:1 |
 如图所示,水平地面上放着一块木板,上面放一个木块,设木块对木板的压力为N,木块所受摩擦力为f.若使木块的B端逐渐升高时,A端不动,木块仍静止,则下列说法正确的是( )
如图所示,水平地面上放着一块木板,上面放一个木块,设木块对木板的压力为N,木块所受摩擦力为f.若使木块的B端逐渐升高时,A端不动,木块仍静止,则下列说法正确的是( )| A. | N增大,f增大 | B. | N增大,f减小 | C. | N减小,f增大 | D. | N减小,f减小 |
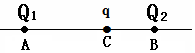 在相距L=1.2m的A、B两点各放一个点电荷Q1、Q2,Q1=+4.0×10-6C,在AB之间距B点0.4m的C点放入一个电量q=1.0×10-6C的点电荷,受力恰好平衡.则Q2应该带正电(填“正”或“负”),电量为1.0×10-6C.
在相距L=1.2m的A、B两点各放一个点电荷Q1、Q2,Q1=+4.0×10-6C,在AB之间距B点0.4m的C点放入一个电量q=1.0×10-6C的点电荷,受力恰好平衡.则Q2应该带正电(填“正”或“负”),电量为1.0×10-6C.
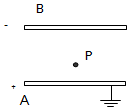 如图所示,已知平行板电容器两极板间距离d=5mm,充电后两极板电势差200V,A板带正电,若电容C=3μF,且P到B板的距离为3mm,求:
如图所示,已知平行板电容器两极板间距离d=5mm,充电后两极板电势差200V,A板带正电,若电容C=3μF,且P到B板的距离为3mm,求: