题目内容
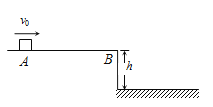
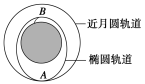
【题目】(多选)我国研制的“嫦娥三号”月球探测器成功在月球表面实现软着陆．如图所示，探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动，之后在轨道上的A点实施变轨，使探测器绕月球做椭圆运动，当运动到B点时继续变轨，使探测器靠近月球表面，当其距离月球表面附近高度为h(h<5m)时开始做自由落体运动，探测器携带的传感器测得自由落体运动时间为t，已知月球半径为R，万有引力常量为G.则下列说法正确的是( )
A．“嫦娥三号”的发射速度必须大于第一宇宙速度
B．探测器在近月圆轨道和椭圆轨道上的周期相等
C．“嫦娥三号”在A点变轨时，需减速才能从近月圆轨道进入椭圆轨道
D．月球的平均密度为
【答案】ACD
【解析】“嫦娥三号”在地表的发射速度大于第一宇宙速度小于第二宇宙速度，A项正确；椭圆轨道的轨道半长轴和近月圆轨道的轨道半径不相等，因此周期不相同，B项错误；从近月圆轨道需要点火减速才能进入椭圆轨道，C项正确；月球质量M＝
，除以体积得到月球密度ρ＝
，根据自由落体运动下落高度为h，运动时间为t，有h＝
gt2得到g＝
代入上述密度表达式中，ρ＝，D项正确．
【题目】某同学利用竖直上抛小球的频闪照片验证机械能守恒定律。频闪仪每隔0.05 s闪光一次，图实中所标数据为实际距离，该同学通过计算得到不同时刻的速度如下表(当地重力加速度取10 m/s2，小球质量m＝0.2 kg，结果保留三位有效数字)：
时刻 | t2 | t3 | t4 | t5 |
速度(m/s) | 5.59 | 5.08 | 4.58 |
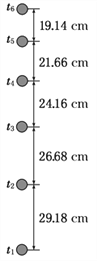
(1)由频闪照片上的数据计算t5时刻小球的速度v5＝________ m/s。
(2)从t2到t5时间内，重力势能增加量ΔEp＝________J，
动能减小量ΔEk＝________J。
(3)在误差允许的范围内，若ΔEp与ΔEk近似相等，从而验证了机械能守恒定律。由上述计算得ΔEp________ΔEk(选填“>”“<”或“＝”)，造成这种结果的主要原因是________________。
