题目内容
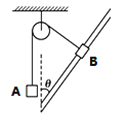
【题目】如图所示,在方向竖直向上、大小E=1ⅹ106V/m的匀强电场中,固定一个穿有A、B两个小球(均视为质点)的光滑绝缘圆环,圆环在竖直平面内,圆心为O、半径R=0. 2m。A、B用一根绝缘轻杆相连,B球带电荷量q=+7ⅹl0-6C,A球不带电,质量分别为mA=0.lkg、mB=0.8kg。将两小球从圆环上的图示位置(A与圆心O等高,B在圆心0的正下方)由静止释放,重力加速度大小为g= l0m/s2。则
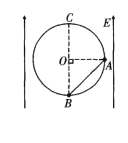
A. 小球A和B受到的合力的大小相等
B. 小球B不能到达圆环的最高点
C. 小球A和B的速度大小始终相等
D. 两小球及轻杆组成的系统最大动能为![]()
【答案】BCD
【解析】
A、B做圆周运动的半径和角速度均相同,对A、B分别由动能定理列方程联立求解最大动能,
AC、设B转过α角时,A、B的速度分别为vA、vB,因A、B做圆周运动的半径和角速度均相同,故vA=vB,所以小球A和B切向加速度大小和法向加速度大小相等,但两球的质量不等,根据牛顿第二定律可知小球A和B受到合力大小不等,故A错误,C正确;
B、设B到达圆环最高点时A、B的动能分别为EKA、EKB,对A根据动能定理有:![]() ,对B根据动能定理有:
,对B根据动能定理有:![]() ,联立解得:
,联立解得:![]() ,上式表明:B在圆环最高点时,系统动能为负值,所以B不能到达圆环最高点,故B正确;
,上式表明:B在圆环最高点时,系统动能为负值,所以B不能到达圆环最高点,故B正确;
D、对A由动能定理:![]() ,对B,由动能定理:
,对B,由动能定理:![]() ,联立解得:
,联立解得:![]() ,据此式知,当
,据此式知,当![]() 时,两小球及轻杆组成的系统最大动能是
时,两小球及轻杆组成的系统最大动能是![]() ,故D正确;
,故D正确;
故选BCD。

练习册系列答案
相关题目