题目内容
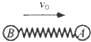
如图所示,光滑地面上有P、Q两个固定挡板,A、B是两挡板连线的三等分点.A点有一质量为m2的静止小球,P挡板的右侧有一质量为m1的等大小球以速度v0向右运动.小球与小球、小球与挡板间的碰撞均没有机械能损失,两小球均可视为质点.已知两小球之间的第二次碰撞恰好发生在B点处,则两小球的质量之比m1:m2可能为( )

| A.3:1 | B.1:3 | C.1:5 | D.1:7 |

①若碰后球1的速度方向与原来的方向相同,可知1球的速度小于2球的速度,两球在B点相遇,是球2反弹后在B点相遇,有:v2t=3v1t,即:v2=3v1.
根据动量守恒得,m1v0=m1v1+m2v2,根据机械能守恒得:
m1v02=
m1v12+
m2v22,
联立解得m1=3m2.故A正确.
②若碰撞后球1的速度方向与原来的方向相反,与挡板碰后反弹在B点追上球2,
则有:v1t=3v2t,即:v1=3v2.
根据动量守恒得:m1v0=-m1v1+m2v2,
根据机械能守恒得:
m1v02=
m1v12+
m2v22,
联立解得:m2=7m1.故D正确.
③若碰撞后球1的速度方向与原来的方向相反,与挡板碰后反弹、球2与单摆碰后反弹在B点相遇,
则有:v1t=v2t,即:v1=v2,
根据动量守恒得:m1v0=-m1v1+m2v2,
根据机械能守恒得:
m1v02=
m1v12+
m2v22,
联立解得:m2=3m1.故B正确.
故选:ABD.
根据动量守恒得,m1v0=m1v1+m2v2,根据机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立解得m1=3m2.故A正确.
②若碰撞后球1的速度方向与原来的方向相反,与挡板碰后反弹在B点追上球2,
则有:v1t=3v2t,即:v1=3v2.
根据动量守恒得:m1v0=-m1v1+m2v2,
根据机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立解得:m2=7m1.故D正确.
③若碰撞后球1的速度方向与原来的方向相反,与挡板碰后反弹、球2与单摆碰后反弹在B点相遇,
则有:v1t=v2t,即:v1=v2,
根据动量守恒得:m1v0=-m1v1+m2v2,
根据机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立解得:m2=3m1.故B正确.
故选:ABD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目