题目内容
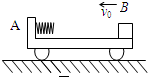
光滑水平面上停着一辆长为L的平板车，车的一端放着质量为m的木箱，车的另一端站着质量为3m的人，车的质量为5m，若人沿车面走到木箱处将木箱搬放到车的正中央，则在这段时间内，车的位移大小为______．
人从车的一端走到另一端时，设车的位移为x1，则人的位移为L-x1，
由动量守恒定律得：3m
-（m+5m）
=0，解得：x1=
；
人搬着箱子走到车正中央时，设车的位移为x2，则人的位移为
L-x2，
由动量守恒定律得：（3m+m）
-5m
=0，解得：x2=
，
整个过程，车的位移x=x1-x2=
-
=
；
故答案为：
．
由动量守恒定律得：3m
| L-x1 |
| t1 |
| x1 |
| t1 |
| L |
| 3 |
人搬着箱子走到车正中央时，设车的位移为x2，则人的位移为
| 1 |
| 2 |
由动量守恒定律得：（3m+m）
| ||
| t2 |
| x2 |
| t2 |
| 2L |
| 9 |
整个过程，车的位移x=x1-x2=
| L |
| 3 |
| 2L |
| 9 |
| L |
| 9 |
故答案为：
| L |
| 9 |
练习册系列答案
相关题目
